题目内容
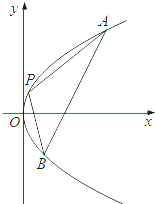
如图,已知焦点在x轴上的椭圆
+
=1(b>0)经过点M(4,1),直线l:y=x+m交椭圆于A,B两不同的点.
(1)求该椭圆的标准方程;
(2)求实数m的取值范围;
(3)是否存在实数m,使△ABM为直角三角形,若存在,求出m的值,若不存,请说明理由.

| x2 |
| 20 |
| y2 |
| b2 |
(1)求该椭圆的标准方程;
(2)求实数m的取值范围;
(3)是否存在实数m,使△ABM为直角三角形,若存在,求出m的值,若不存,请说明理由.

(1)依题意
+
=1,解得b2=5,…(2分)
所以椭圆的标准方程是
+
=1.…(3分)
(2)由
得5x2+8mx+4m2-20=0,…(4分)
∵直线l与椭圆有两个不同的交点,
∴△=(8m)2-20(4m2-20)=-16m2+400>0…(6分)
解得-5<m<5.…(7分)
(3)假设存在实数m满足题意,
当MA⊥AB时,直线MA的方程为y-1=-(x-4),即y=-x+5.
由
得x2-8x+16=0,解得
.
故A(4,1),与点M重合,不合题意.
同理,当MB⊥AB时,也不合题意.…(9分)
当MA⊥MB时,设A(x1,y1),B(x2,y2).
由(2)得x1+x2=-
,x1•x2=
,
y1+y2=x1+x2+2m,y1•y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2.…(10分)
∵
=(x1-4,y1-1),
=(x2-4,y2-1)
∴
•
=(x1-4)(x2-4)+(y1-1)(y2-1)…(11分)
=x1x2-4(x1+x2)+16+y1y2-(y1+y2)+1
=2x1x2+(m-5)(x1+x2)+m2-2m+17
=2•
+(m-5)(-
)+m2-2m+17
=
+m2-2m+17=m2+6m+9.…(13分)
又
•
=0,
∴m2+6m+9=0,
解得m=-3∈(-5,5),
综上所述,存在实数m=-3使△ABM为直角三角形.…(14分)
| 16 |
| 20 |
| 1 |
| b2 |
所以椭圆的标准方程是
| x2 |
| 20 |
| y2 |
| 5 |
(2)由
|
∵直线l与椭圆有两个不同的交点,
∴△=(8m)2-20(4m2-20)=-16m2+400>0…(6分)
解得-5<m<5.…(7分)
(3)假设存在实数m满足题意,
当MA⊥AB时,直线MA的方程为y-1=-(x-4),即y=-x+5.
由
|
|
故A(4,1),与点M重合,不合题意.
同理,当MB⊥AB时,也不合题意.…(9分)
当MA⊥MB时,设A(x1,y1),B(x2,y2).
由(2)得x1+x2=-
| 8m |
| 5 |
| 4m2-20 |
| 5 |
y1+y2=x1+x2+2m,y1•y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2.…(10分)
∵
| MA |
| MB |
∴
| MA |
| MB |
=x1x2-4(x1+x2)+16+y1y2-(y1+y2)+1
=2x1x2+(m-5)(x1+x2)+m2-2m+17
=2•
| 4m2-20 |
| 5 |
| 8m |
| 5 |
=
| 40m-40 |
| 5 |
又
| MA |
| MB |
∴m2+6m+9=0,
解得m=-3∈(-5,5),
综上所述,存在实数m=-3使△ABM为直角三角形.…(14分)

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目