题目内容
【题目】如图所示,椭圆![]() 离心率为
离心率为![]() ,
,![]() 、
、![]() 是椭圆C的短轴端点,且
是椭圆C的短轴端点,且![]() 到焦点的距离为
到焦点的距离为![]() ,点M在椭圆C上运动,且点M不与
,点M在椭圆C上运动,且点M不与![]() 、
、![]() 重合,点N满足
重合,点N满足![]() .
.

(1)求椭圆C的方程;
(2)求四边形![]() 面积的最大值.
面积的最大值.
【答案】![]()
![]() ;
;![]()
![]() .
.
【解析】
![]() 根据离心率和
根据离心率和![]() 的长度求得
的长度求得![]() ,从而得到椭圆方程;
,从而得到椭圆方程;![]() 四边形
四边形![]() 的面积可以表示为:
的面积可以表示为:![]() ,通过假设直线分别求得
,通过假设直线分别求得![]() 和
和![]() ,从而将问题转化为函数最值求解问题,从而得到结果.根据不同的假设直线的方式,会构成不同的函数,得到不同的解法.
,从而将问题转化为函数最值求解问题,从而得到结果.根据不同的假设直线的方式,会构成不同的函数,得到不同的解法.
![]()
![]()
![]()
又![]() 且
且![]() ,解得:
,解得:![]() ,
,![]()
因此椭圆![]() 的方程为
的方程为![]()
![]() 法一:设
法一:设![]() ,
,![]()
![]() ,
,![]()
![]() 直线
直线![]() ……①;直线
……①;直线![]() ……②
……②
由①②解得:![]()
又![]()
![]()
四边形![]() 的面积
的面积![]()
![]()
![]() 当
当![]() 时,
时,![]() 的最大值为
的最大值为![]()
法二:设直线![]() ,则直线
,则直线![]() ……①
……①
直线![]() 与椭圆
与椭圆![]() 的交点
的交点![]() 的坐标为
的坐标为![]()
则直线![]() 的斜率为
的斜率为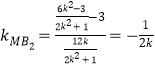
![]() 直线
直线![]() ……②
……②
由①②解得:![]()
四边形![]() 的面积:
的面积:![]()
当且仅当![]() 时,
时,![]() 取得最大值
取得最大值![]()

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目

