Question

【题目】如图，已知三棱锥，点是的中点，且，，过点作一个截面，使截面平行于和，则截面的周长为（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

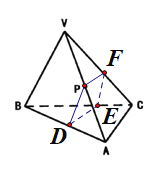
如图所示，设AB、BC、VC的中点分别为D,E,F，连接PD,DE,EF,PF.先证明截面DEFP就是所作的平面，再求截面的周长.

如图所示，设AB、BC、VC的中点分别为D,E,F，连接PD,DE,EF,PF.

由题得PD||VB,DE||AC,

因为平面DEFP,VB,AC不在平面DEFP内，

所以VB||平面DEFP,AC||平面DEFP,

所以截面DEFP就是所作的平面.

由于,

所以四边形DEFP是平行四边形，

因为VB=4,AC=2,所以PD=FE=2,DE=PF=1,

所以截面DEFP的周长为2+2+1+1=6.

故选：D