题目内容
17.已知:E是正方形ABCD的AB边延长线上一点,DE交CB于M,MN∥AE.求证:MN=MB.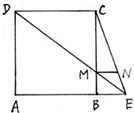
分析 证明MN∥CD,利用比例,即可证明结论.
解答 证明:因为正方形ABCD,所以AE∥CD
因为MN∥AE,所以MN∥CD
所以MN:CD=EM:ED,BM:AD=EM:ED
因为在正方形里CD=AD
所以MN=BM.
点评 本题考查平行线的性质,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
12.若α为第一象限角,则$\frac{α}{2}$为( )
| A. | 第一象限的角 | B. | 第一或第四象限的角 | ||
| C. | 第一或第三象限的角 | D. | 第二或第四象限的角 |
2.户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,决定从本单位中抽取50人进行问卷调查,得到了如下列联表:
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜欢户外运动与性别有关?并说明你的理由.
下面的临界值表仅供参考:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 喜欢户外运动 | 不喜欢户外运动 | 合计 | |
| 男性 | 5 | ||
| 女性 | 10 | 25 | |
| 合计 | 30 | 50 |
(2)是否有99.5%的把握认为喜欢户外运动与性别有关?并说明你的理由.
下面的临界值表仅供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9.i是虚数单位,$\frac{(-1+i)(2+i)}{{i}^{3}}$的虚部为( )
| A. | -3 | B. | -i | C. | -1 | D. | -3i |
6.甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.
(1)请填写如表:
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(谁的成绩更稳定);
②从折线图上两人射击命中环数的走势看(谁更有潜力).

(1)请填写如表:
| 平均数 | 方差 | 中位数 | 命中9环及9环以上的次数 | |
| 甲 | ||||
| 乙 |
①从平均数和方差相结合看(谁的成绩更稳定);
②从折线图上两人射击命中环数的走势看(谁更有潜力).