题目内容
8．函数f（x）=cos2x-2$\sqrt{3}$sinxcosx的最小正周期是π．分析 利用三角函数的恒等变换化简函数的解析式，再利用余弦函数的周期性得出结论．
解答 解：函数f（x）=cos2x-2$\sqrt{3}$sinxcosx=cos2x-$\sqrt{3}$sin2x=2cos（2x+$\frac{π}{3}$）的最小正周期为$\frac{2π}{2}$=π，
故答案为：π．
点评 本题主要考查三角函数的恒等变换及化简求值，余弦函数的周期性和求法，属于基础题．
练习册系列答案
小学课时特训系列答案
相关题目
19．曲线y=x3在点（1，1）处的切线与x轴、直线x=2所围成的三角形的面积为（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{7}{3}$ | C． | $\frac{5}{3}$ | D． | $\frac{4}{3}$ |
3．化简：sin（$\frac{4n-1}{4}$π-α）+cos（$\frac{4n+1}{4}$π-α）（n∈Z）值（ ）
| A． | 2sinа | B． | 2cosа | C． | 0 | D． | -2sinа |
13．某交互式计算机有20个终端，这些终端由各个单位独立操作，使用率均为0.8，则20个终端中至少有一个没有使用的概率为（ ）
| A． | 0.220 | B． | 0.820 | C． | 1-0.820 | D． | 1-0.220 |
20．在△ABC中，角A、B、C、的对边分别为a、b、c，（a+b）（cosA+cosB）=2c，则△ABC（ ）
| A． | 是等腰三角形，但不一定是直角三角形 | |
| B． | 是直角三角形，但不一定是等腰三角形 | |
| C． | 既不是等腰三角形，也不是直角三角形 | |
| D． | 既不是等腰三角形，也是直角三角形 |
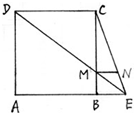
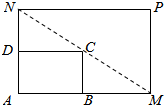如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求M在AB的延长线上，N在AD的延长线上，且对角线MN过C点．已知AB=3米，AD=2米．设AN=x（单位：米），若x∈[3，4]（单位：米），则当AM，AN的长度分别是多少时，花坛AMPN的面积最大？并求出最大面积．