��Ŀ����
2����ʵ��a��b��c��d�ų�$��{\begin{array}{l}a&c\\ b&d\end{array}}��$����ʽ����Ϊ���ж��о����ڵ�P��x��y������������һ������$��{x��y}����{\begin{array}{l}a&c\\ b&d\end{array}}��=��{ax+by��cx+dy}��$�����ƣ�ax+by��cx+dy��Ϊ��P�ھ���$��{\begin{array}{l}a&c\\ b&d\end{array}}��$�����µĵ㣮�����������⣺�ٵ�P��3��4���ھ���$��\begin{array}{l}{1}&{2}\\{0}&{1}\end{array}��$�����µĵ�Ϊ��3��10����
������y=x2�ϵĵ��ھ���$��\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}��$�������½����㷽��y=-x2��
�۷�����$\left\{\begin{array}{l}{{a}_{11}x+{a}_{12}y={b}_{1}}\\{{a}_{21}x+{a}_{22}y={b}_{2}}\end{array}\right.$�ɱ�ʾ�ɾ������㣨x��y��$��\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}��$=��b1��b2����
��������x2+4xy+2y2=1��$��\begin{array}{l}{1}&{a}\\{b}&{1}\end{array}��$�����±任������x2-2y2=1����a+b=2��
��������������Ϊ�٢ܣ��������������������ţ�
���� �٣�3��4��$��\begin{array}{l}{1}&{2}\\{0}&{1}\end{array}��$=��3��1+4��0��3��2+4��1��=��3��10�����Ӷ��жϣ�
��������y=x2�ϵĵ�Ϊ��x1��y1�����ھ���$��\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}��$�������µĵ�Ϊ��x��y������x1��y1��$��\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}��$=��x1��y1��=��x��y�����Ӷ��жϣ�
�ۣ�x��y��$��\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}��$=��xa11+ya21��xa12+ya22�����Ӷ��жϣ�
��x2+4xy+2y2=1�ɻ�Ϊ��x+2y��2-2y2=1���Ӷ��ɵã�x��y��$��\begin{array}{l}{1}&{a}\\{b}&{1}\end{array}��$=��x+2y��y�����Ӷ���a��b��
��� �⣺�١ߣ�3��4��$��\begin{array}{l}{1}&{2}\\{0}&{1}\end{array}��$=��3��1+4��0��3��2+4��1��=��3��10����
���P��3��4���ھ���$��\begin{array}{l}{1}&{2}\\{0}&{1}\end{array}��$�����µĵ�Ϊ��3��10���������⣻
��������y=x2�ϵĵ�Ϊ��x1��y1�����ھ���$��\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}��$�������µĵ�Ϊ��x��y����
��x1��y1��$��\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}��$=��x1��y1��=��x��y����
�����㷽��y=x2��
�ʢ��Ǽ����⣻
�ۣ�x��y��$��\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}��$=��xa11+ya21��xa12+ya22����
�ʢ��Ǽ����⣻
��x2+4xy+2y2=1�ɻ�Ϊ��x+2y��2-2y2=1��
��x��y��$��\begin{array}{l}{1}&{a}\\{b}&{1}\end{array}��$=��x+2y��y����
��b=2��a=0��
��a+b=2��
�ʢ��������⣻
�ʴ�Ϊ���٢ܣ�
���� ���⿼���˾�����任��Ӧ�ã����ڻ����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | $\frac{5}{2}$ | B�� | 4 | C�� | $\frac{9}{2}$ | D�� | 9 |
| A�� | $\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-3}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-3}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{b=3}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=3}\end{array}\right.$ |
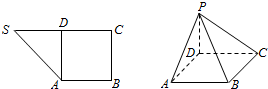 ��ͼ1����ֱ������SABC�У���B=��C=$\frac{��}{2}$��DΪ��SC�ϵĵ㣬��AD��SC���ֽ���SAD��AD����PAD��λ�ã�������S��ΪP������ʹ��PA��AB��
��ͼ1����ֱ������SABC�У���B=��C=$\frac{��}{2}$��DΪ��SC�ϵĵ㣬��AD��SC���ֽ���SAD��AD����PAD��λ�ã�������S��ΪP������ʹ��PA��AB�� ������P-ABCD�У�����ABCD��ֱ�����Σ�AB��DC����ABC=$\frac{��}{2}$��AD=2$\sqrt{2}$��AB=3DC=3��
������P-ABCD�У�����ABCD��ֱ�����Σ�AB��DC����ABC=$\frac{��}{2}$��AD=2$\sqrt{2}$��AB=3DC=3��
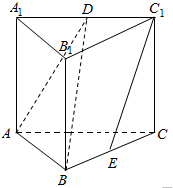 ֱ������ABC-A1B1C1�У�AA1=AC��AB��AC��D��E�ֱ���A1C1��BC���е㣮
ֱ������ABC-A1B1C1�У�AA1=AC��AB��AC��D��E�ֱ���A1C1��BC���е㣮