题目内容
【题目】设函数f(x)= ![]() (Ⅰ)当
(Ⅰ)当 ![]() 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(Ⅱ)若函数f(x)是(﹣∞,+∞)上的减函数,求实数a的取值范围.
【答案】解:(Ⅰ)a= ![]() 时,f(x)=
时,f(x)= 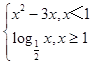 , 当x<1时,f(x)=x2﹣3x是减函数,所以f(x)>f(1)=﹣2,即x<1时,f(x)的值域是(﹣2,+∞).
, 当x<1时,f(x)=x2﹣3x是减函数,所以f(x)>f(1)=﹣2,即x<1时,f(x)的值域是(﹣2,+∞).
当x≥1时,f(x)= ![]() 是减函数,所以f(x)≤f(1)=0,即x≥1时,f(x)的值域是(﹣∞,0].
是减函数,所以f(x)≤f(1)=0,即x≥1时,f(x)的值域是(﹣∞,0].
于是函数f(x)的值域是(﹣∞,0]∪(﹣2,+∞)=R.
(Ⅱ)若函数f(x)是(﹣∞,+∞)上的减函数,则下列①②③三个条件同时成立:
①当x<1,f(x)=x2﹣(4a+1)x﹣8a+4是减函数,于是 ![]() ≥1,则a≥
≥1,则a≥ ![]() .
.
②x≥1时,f(x)= ![]() 是减函数,则0<a<1.
是减函数,则0<a<1.
③12﹣(4a+1)1﹣8a+4≥0,则a≤ ![]() .
.
于是实数a的取值范围是[ ![]() ,
, ![]() ]
]
【解析】(Ⅰ)a= ![]() 时,f(x)=
时,f(x)= 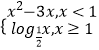 ,当x<1时,f(x)=x2﹣3x是减函数,可求此时函数f(x)的值域;同理可求得当x≥1时,减函数f(x)=
,当x<1时,f(x)=x2﹣3x是减函数,可求此时函数f(x)的值域;同理可求得当x≥1时,减函数f(x)= ![]() 的值域;(Ⅱ)函数f(x)是(﹣∞,+∞)上的减函数,三个条件需同时成立,①
的值域;(Ⅱ)函数f(x)是(﹣∞,+∞)上的减函数,三个条件需同时成立,① ![]() ≥1,②0<a<1,③12﹣(4a+1)1﹣8a+4≥0,从而可解得实数a的取值范围.
≥1,②0<a<1,③12﹣(4a+1)1﹣8a+4≥0,从而可解得实数a的取值范围.
【考点精析】认真审题,首先需要了解函数单调性的性质(函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集),还要掌握函数的值(函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法)的相关知识才是答题的关键.

练习册系列答案
相关题目
