Question

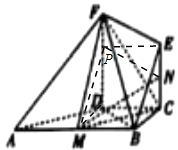
【题目】如图，在直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=2，AB=4，EC∥FD，FD⊥底面ABCD，M是AB的中点．

（1）求证：平面CFM⊥平面BDF；
（2）若点N为线段CE的中点，EC=2，FD=3，求证：MN∥平面BEF．

Answer 1

【答案】
（1）

证明：直角梯形ABCD中，AB∥CD，BC=2，AB=4，且M是AB的中点，

∴BM=CD，∴四边形BCDM是平行四边形，

又BC=CD=2，∴平行四边形BCDM是菱形；

∴BD⊥CM，

又FD⊥底面ABCD，CM平面BCDM，∴FD⊥CM，

且FD∩BD=D，

∴CM⊥平面BDF，

有CM平面CFM，

∴平面CFM⊥平面BDF；

（2）

过点N作NP∥EF，交DF与点P，连接PM，如图所示；

∵EC∥FD，∴四边形EFPN是平行四边形，

又点N为线段CE的中点，EC=2，FD=3，

∴FP= EC=1，

PD=EC=2，

∴PE∥CD，且PE=CD，

又BM∥CD，且BM=CD，

∴BM∥PE，且PE=BM，

∴四边形BEPM为平行四边形，

∴PM∥BE；

又PM平面BEF，BE平面BEF，∴PM∥平面BEF；

同理，PM∥平面BEF，

又PM∩PN=P，PM平面PMN，PN平面PMN，

∴平面PMN∥平面BEF，

又MN平面PMN，∴MN∥平面BEF．

【解析】（1）证明四边形BCDM是菱形，对角线BD⊥CM，再证明FD⊥CM，即可证明CM⊥平面BDF，从而得平面CFM⊥平面BDF；（2）过点N作NP∥EF，交DF与点P，连接PM，证明平面PMN∥平面BEF，即可证明MN∥平面BEF．
【考点精析】认真审题，首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行)，还要掌握平面与平面垂直的判定(一个平面过另一个平面的垂线，则这两个平面垂直)的相关知识才是答题的关键．