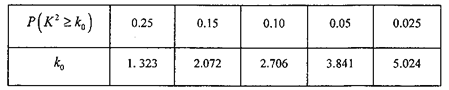
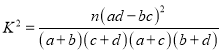题目内容
【题目】设fn(x)=(3n﹣1)x2﹣x(n∈N*),An={x|fn(x)<0}
(1)定义An={x|x1<x<x2}的长度为x2﹣x1 , 求An的长度;
(2)把An的长度记作数列{an},令bn=anan+1;
1°求数列{bn}的前n项和Sn;
2°是否存在正整数m,n(1<m<n),使得S1 , Sm , Sn成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
【答案】
(1)解:由fn(x)<0得(3n﹣1)x2﹣x<0,∴0<x< ![]() ,
,
∴An的长度为 ![]()
(2)解:1°、an= ![]() ,bn=anan+1=
,bn=anan+1= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
∴数列{bn}的前n项和Sn= ![]() [(
[( ![]() ﹣
﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() )]=
)]= ![]() ;
;
2°、由1°可知S1= ![]() ,Sm=
,Sm= ![]() ,Sn=
,Sn= ![]() ,
,
假设存在正整数m,n(1<m<n),使得S1,Sm,Sn成等比数列,
则Sm2=S1Sn,化简得(﹣3m2+6m+2)n=5m2,
m=2时,n=10;
m≥3时,﹣3m2+6m+2<0,5m2>0,等式不成立,
综上所述,存在正整数m=2,n=10,使得S1,Sm,Sn成等比数列
【解析】(1)利用新定义,即可求An的长度;(2)1°利用裂项法可求得Sn;
2°假设存在正整数m、n,且1<m<n,使得S1、Sm、Sn成等比数列,可求得(﹣3m2+6m+2)n=5m2 , 由1<m<n,验证可求得结论.
【考点精析】通过灵活运用二次函数的性质,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减即可以解答此题.
上递减即可以解答此题.

练习册系列答案
相关题目