Question

【题目】已知定义在（﹣1，1）上的函数f（x）满足：对任意x，y∈（﹣1，1）都有f（x）+f（y）=f（x+y）．
（Ⅰ）求证：函数f（x）是奇函数；
（Ⅱ）如果当x∈（﹣1，0]时，有f（x）＜0，试判断f（x）在（﹣1，1）上的单调性，并用定义证明你的判断；
（Ⅲ）在（Ⅱ）的条件下，若a﹣8x+1＞0对满足不等式f（x﹣ ）+f（ ﹣2x）＜0的任意x恒成立，求a的取值范围．

Answer 1

【答案】解：（Ⅰ）由题可知，函数y=f（x）的定义域为（﹣1，1），关于原点对称；对于f（x）+f（y）=f（x+y）．
令y=x=0，可得2f（0）=f（0），从而f（0）=0，
再令y=﹣x，可得f（x）+f（﹣x）=f（0）=0，即f（﹣x）=﹣f（x），
所以y=f（x）为（﹣1，1）上的奇函数；
（Ⅱ）y=f（x）为（﹣1，1）上单调递增，
证明如下：
设x1、x2为区间（﹣1，0]上的任意两个自变量的值，且x1＜x2 ，
则f（x1）﹣f（x2）=f（x1）+f（﹣x2）=f（x1﹣x2）；
由于﹣1＜x1＜x2＜0，所以﹣1＜x1﹣x2≤0，从而f（x1﹣x2）＜0，
即f（x1）＜f（x2），所以y=f（x）为（﹣1，0]上单调递增，
又由于y=f（x）为（﹣1，1）上的奇函数；
由奇函数的性质分析可得：y=f（x）为[0，1）上单调递增，
故y=f（x）为（﹣1，1）上单调递增，
（Ⅲ）根据题意，若f（x﹣ ）+f（ ﹣2x）＜0，
则有f（x﹣ ）＜f（2x﹣ ），
则必有 ，
解可得﹣ ＜x＜ ，
所以原问题等价于a﹣8x+1＞0对于﹣ ＜x＜ 恒成立，
则必有a≥[8×（ ）﹣1]=4，即a≥4；
故a的取值范围是[4，+∞）
【解析】（Ⅰ）根据题意，先分析函数的定义域，可得其定义域关于原点对称，进而令y=x=0，可得f（0）=0，再令y=﹣x，分析可得f（﹣x）=﹣f（x），即可得答案；（Ⅱ）分析可得：y=f（x）为（﹣1，1）上单调递增，进而证明：先用定义法证明可得y=f（x）为（﹣1，0]上单调递增，进而结合函数的奇偶性可得y=f（x）为（﹣1，0]上单调递增，综合可得答案；（Ⅲ）根据题意，由函数的奇偶性以及单调性可得：若f（x﹣ ）+f（ ﹣2x）＜0，则必有 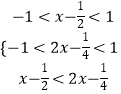，解可得x的范围，所以原问题等价于a﹣8x+1＞0对于﹣ ＜x＜ 恒成立，分析可得a的取值范围，即可得答案．
【考点精析】利用函数奇偶性的性质对题目进行判断即可得到答案，需要熟知在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇．