题目内容
1.已知点P(x,y)是圆x2+y2=5上任意一点,若z=y-$\sqrt{3}$x,那么z的取值范围[-2$\sqrt{5}$,2$\sqrt{5}$].分析 利用圆的参数方程,结合辅助角公式,即可得出结论.
解答 解:由题意,设x=$\sqrt{5}$cosα,y=$\sqrt{5}$sinα,
则z=y-$\sqrt{3}$x=$\sqrt{5}$sinα-$\sqrt{15}$cosα=2$\sqrt{5}$sin(α-$\frac{π}{6}$),
∴-2$\sqrt{5}$≤z≤2$\sqrt{5}$.
故答案为:[-2$\sqrt{5}$,2$\sqrt{5}$].
点评 本题考查圆的方程,考查辅助角公式,正确运用圆的参数方程是关键.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
16.已知△ABC的三个顶点ABC及所在平面内一点,P满足$\overrightarrow{PA}$+$\overrightarrow{PB}$+2$\overrightarrow{PC}$=$\overrightarrow{CB}$,则点P与△ABC的关系为( )
| A. | P在△ABC内部 | B. | P在AB边所在直线上 | ||
| C. | P在BC边所在直线上 | D. | P在AC边所在直线上 |
10.集合A={y|y=2x,x∈R},B={-1,0,1},则下列结论正确的是( )
| A. | A∪B=(0,+∞) | B. | (∁RA)∪B=(-∞,0] | C. | (∁RA)∩B={-1,0} | D. | (∁RA)∩B={1} |
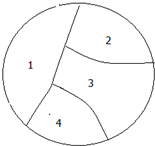 用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.
用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.