题目内容
8．已知f（x）是定义在R上的偶函数，若命题p：?x∈R，f（-x）=f（|x|），则?p为（ ）| A． | ?x0∈R，f（-x0）≠f（|x0|） | B． | ?x∈R，f（-x）≠f（|x|） | ||
| C． | ?x0∈R，f（-x0）=f（|x0|） | D． | 不存在x0∈R，f（-x0）=f（|x0|） |
分析 直接利用命题的否定写出结果即可．
解答 解：因为全称命题的否定是特称命题，所以若命题p：?x∈R，f（-x）=f（|x|），则?p为：?x0∈R，f（-x0）≠f（|x0|）．
故选：A．
点评 本题考查命题的否定，全称命题与特称命题的否定关系，基本知识的考查．
练习册系列答案
相关题目
16．函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则ω，φ的值分别为（ ）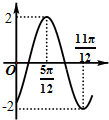
| A． | 2，-$\frac{π}{3}$ | B． | 2，-$\frac{π}{6}$ | C． | 4，-$\frac{π}{6}$ | D． | 4，$\frac{π}{3}$ |
3．
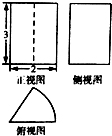某由圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为60°的扇形，则该几何体的体积为（ ）
某由圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为60°的扇形，则该几何体的体积为（ ）| A． | 2π | B． | π | C． | $\frac{2π}{3}$ | D． | $\frac{π}{3}$ |
13．由动点 P向圆x2+y2=1引两条切线，切点分别为 A、B，若$\overrightarrow{{P}{A}}$•$\overrightarrow{{P}{B}}$=$\frac{3}{2}$，则动点 P的轨迹方程为（ ）
| A． | x2+y2=2 | B． | x2+y2=$\frac{9}{4}$ | C． | x2+y2=4 | D． | x2+y2=9 |
20．七位裁判各自对一名跳水运动员打分后，去掉一个最高分，再去掉一个最低分，关于剩余分数的说法一定正确的是（ ）
| A． | 众数不变 | B． | 方差不变 | C． | 平均值不变 | D． | 中位数不变 |