题目内容

4．已知函数f（x）=x3-3x2+a，若f（x+1）是奇函数，则曲线y=f（x）在点（0，a）处的切线方程是（　　）
A．x=0B．x=2C．y=2D．y=4

分析 运用奇函数的性质，若f（x+1）是奇函数，则f（1）=0，求得a，再求函数的导数，求出切线的斜率，运用点斜式方程，即可得到切线方程．

解答 解：由于函数f（x）=x3-3x2+a，若f（x+1）是奇函数，
则f（1）=0，即有1-3+a=0，解得，a=2，
f（x）=x3-3x2+2，导数f′（x）=3x2-6x，
则在切点（0，2）处的斜率为0，
则切线方程为：y=2．
故选：C．

点评 本题考查导数的运用：求切线方程，考查函数的奇偶性及运用，考查运算能力，属于基础题．

练习册系列答案
相关题目
6．已知函数f（x）=|x+$\frac{1}{2}$|+|x-$\frac{1}{2}$|，不等式f（x）＜2的解集为M．
（1）求M；
（2）当a、b∈M时，证明：|a+b|＜|1+ab|．
15．直线l过点P（0，2）且与椭圆$\frac{x^2}{2}$+y2=1相交于M，N两点，求△MON面积的最大值．
12．若函数f（x）=x3+x2-2x-2的一个正数零点附近的函数值用二分法计算，其参考数据如下：
f （1）=-2f （1.5）=0.625f （1.25）=-0.984
f （1.375）=-0.260f （1.4375）=0.162f （1.40625）=-0.054
那么方程x3+x2-2x-2=0的一个近似根（精确度为0.05）可以是（　　）
A．1.25B．1.375C．1.42D．1.5
19．椭圆T的中心为坐标原点O，右焦点为F（2，0），且椭圆T过点E（2，$\sqrt{2}$）．△ABC的三个顶点都在椭圆T上，设三条边的中点分别为M，N，P．
（1）求椭圆T的离心率；
（2）设△ABC的三条边所在直线的斜率分别为k1，k2，k3，且ki≠0，i=1，2，3．若直线OM，ON，OP的斜率之和为0，求证：$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$+$\frac{1}{{k}_{3}}$为定值．
9．椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上的点到左准线的距离为5，那么它到右焦点的距离为（　　）
A．$\frac{25}{4}$B．$\frac{15}{2}$C．4D．6
16．函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则ω，φ的值分别为（　　）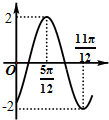
A．2，-$\frac{π}{3}$B．2，-$\frac{π}{6}$C．4，-$\frac{π}{6}$D．4，$\frac{π}{3}$
13．由动点 P向圆x2+y2=1引两条切线，切点分别为 A、B，若$\overrightarrow{{P}{A}}$•$\overrightarrow{{P}{B}}$=$\frac{3}{2}$，则动点 P的轨迹方程为（　　）
A．x2+y2=2B．x2+y2=$\frac{9}{4}$C．x2+y2=4D．x2+y2=9
14．已知函数f（x）=$\left\{\begin{array}{l}a•{2^x}（x≤0）\\{log_2}x（x＞0）\end{array}$，若关于x的方程f[f（x）]=0有且只有一个实数根，则实数a的取值范围是（　　）
A．（-∞，0）B．（-∞，0）∪（0，1）C．（0，1）D．（0，1）∪（1，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网