题目内容
6.在区间(0,π)上随机取一个数x,则事件“sinx+cosx>1”发生的概率为$\frac{1}{2}$.分析 利用三角函数的辅助角公式求出sinx+cosx>1的等价条件,利用几何概型的概率公式即可得到结论.
解答 解:由sinx+cosx>1得$\sqrt{2}$sin(x+$\frac{π}{4}$)>1,
即sin(x+$\frac{π}{4}$)>$\frac{\sqrt{2}}{2}$,
∴$\frac{π}{4}$+2kπ<x+$\frac{π}{4}$<2kπ+$\frac{3π}{4}$,k∈Z,
即2kπ<x<2kπ+$\frac{π}{2}$,k∈Z,
∵0≤x≤π,
∴当k=0时,x的取值范围是0<x<$\frac{π}{2}$,
则“sinx+cosx≤1”发生的概率P=$\frac{\frac{π}{2}-0}{π-0}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 本题主要考查几何概型的概率的计算,利用辅助角公式求出不等式的等价条件是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别为( )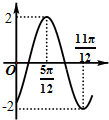

| A. | 2,-$\frac{π}{3}$ | B. | 2,-$\frac{π}{6}$ | C. | 4,-$\frac{π}{6}$ | D. | 4,$\frac{π}{3}$ |
14.已知函数f(x)=$\left\{\begin{array}{l}a•{2^x}(x≤0)\\{log_2}x(x>0)\end{array}$,若关于x的方程f[f(x)]=0有且只有一个实数根,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (-∞,0)∪(0,1) | C. | (0,1) | D. | (0,1)∪(1,+∞) |
1.“x>1”是“︳x|>1”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分又不必要 |
11.已知函数f(x)=(m-2)x2+mx+(2m+1)的两个零点分别在区间(-1,0)和区间(1,2)内,则实数m的取值范围是( )
| A. | [$\frac{1}{4}$,$\frac{1}{2}$] | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,$\frac{1}{4}$) | D. | ($\frac{1}{4}$,$\frac{1}{2}$) |