题目内容
已知奇函数f(x)是定义在R上的增函数,数列{xn}是一个公差为2的等差数列,且满足f(x8)+f(x9)+f(x10)+f(x11)=0,则x2012的值为 .
4005
设x8=a,则x9=a+2,x10=a+4,x11=a+6,
所以f(a)+f(a+2)+f(a+4)+f(a+6)=0,且f(a)<f(a+2)<f(a+4)<f(a+6),
所以f(a)<0且f(a+6)>0.
结合奇函数关于原点的对称性可知,f(a)+f(a+6)=0,f(a+2)+f(a+4)=0,
所以f(a+3)=0=f(0),即a+3=0,所以x8=-3.
设数列{xn}通项xn=x1+2(n-1),所以x8=x1+14=-3,所以x1=-17.
故通项xn=2n-19.所以x2012=2×2012-19=4005.
所以f(a)+f(a+2)+f(a+4)+f(a+6)=0,且f(a)<f(a+2)<f(a+4)<f(a+6),
所以f(a)<0且f(a+6)>0.
结合奇函数关于原点的对称性可知,f(a)+f(a+6)=0,f(a+2)+f(a+4)=0,
所以f(a+3)=0=f(0),即a+3=0,所以x8=-3.
设数列{xn}通项xn=x1+2(n-1),所以x8=x1+14=-3,所以x1=-17.
故通项xn=2n-19.所以x2012=2×2012-19=4005.

练习册系列答案
相关题目
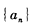 中,
中,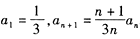
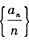 是等比数列,并求
是等比数列,并求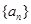 是等差数列,首项
是等差数列,首项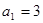 ,前
,前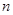 项和为
项和为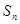 .令
.令 ,
,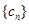 的前
的前 项和
项和 .数列
.数列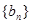 是公比为
是公比为 的等比数列,前
的等比数列,前 ,且
,且 ,
, .
. 的通项公式;
的通项公式;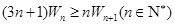 .
. Sn+1,n∈N*.
Sn+1,n∈N*.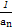 }的前n项和Tn.
}的前n项和Tn.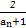 ,且前n项和为Tn,设cn=T2n+1-Tn.
,且前n项和为Tn,设cn=T2n+1-Tn.