题目内容
已知集合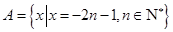 ,
,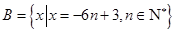 ,设
,设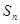 是等差数列
是等差数列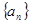 的前
的前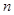 项和,若
项和,若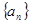 的任一项
的任一项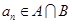 ,且首项
,且首项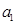 是
是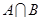 中的最大数,
中的最大数, 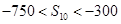 .
.
(1)求数列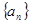 的通项公式;
的通项公式;
(2)若数列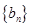 满足
满足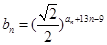 ,求
,求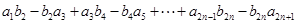 的值.
的值.
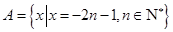 ,
,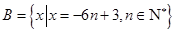 ,设
,设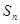 是等差数列
是等差数列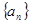 的前
的前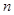 项和,若
项和,若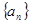 的任一项
的任一项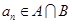 ,且首项
,且首项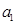 是
是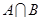 中的最大数,
中的最大数, 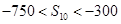 .
.(1)求数列
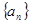 的通项公式;
的通项公式;(2)若数列
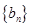 满足
满足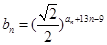 ,求
,求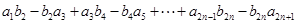 的值.
的值.(1) (
( );(2)
);(2)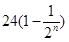 .
.
 (
( );(2)
);(2)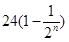 .
.试题分析:(1)首先由题设知: 集合
 中所有元素可以组成以
中所有元素可以组成以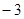 为首项,
为首项,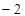 为公差的递减等差数列;集合
为公差的递减等差数列;集合 中所有的元素可以组成以
中所有的元素可以组成以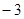 为首项,
为首项, 为公差的递减等差数列.
为公差的递减等差数列.得到
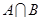 中的最大数为
中的最大数为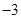 ,得到等差数列的首项
,得到等差数列的首项 .
.通过设等差数列
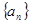 的公差为
的公差为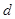 ,建立
,建立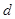 的方程组
的方程组 ,
,
根据
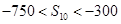 ,求得
,求得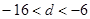
由于
 中所有的元素可以组成以
中所有的元素可以组成以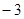 为首项,
为首项, 为公差的递减等差数列,
为公差的递减等差数列,所以
 ,由
,由
 ,得到
,得到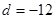 .
.(2)由(1)得到
 ,
,于是
 可化为等比数列的求和
可化为等比数列的求和 .
.试题解析:(1)由题设知: 集合
 中所有元素可以组成以
中所有元素可以组成以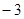 为首项,
为首项,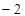 为公差的递减等差数列;集合
为公差的递减等差数列;集合 中所有的元素可以组成以
中所有的元素可以组成以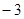 为首项,
为首项, 为公差的递减等差数列.
为公差的递减等差数列.由此可得,对任意的
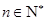 ,有
,有
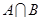 中的最大数为
中的最大数为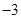 ,即
,即 3分
3分设等差数列
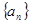 的公差为
的公差为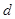 ,则
,则 ,
,
因为
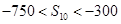 ,
, 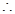
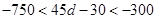 ,即
,即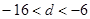
由于
 中所有的元素可以组成以
中所有的元素可以组成以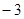 为首项,
为首项, 为公差的递减等差数列,
为公差的递减等差数列,所以
 ,由
,由
 ,所以
,所以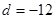
所以数列
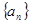 的通项公式为
的通项公式为 (
( ) 8分
) 8分(2)
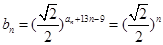 9分
9分于是有


 12分
12分
练习册系列答案
相关题目
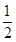 ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.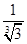 ,公比为
,公比为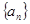 和等比数列
和等比数列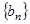 中,
中,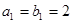 ,
,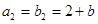 ,
,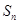 是
是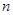 项和.
项和.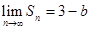 ,求实数
,求实数 的值;
的值;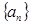 中?若存在,求出所有的
中?若存在,求出所有的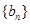 中至少有三项在数列
中至少有三项在数列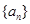 中,但
中,但 ,一个等比中项是
,一个等比中项是 ,且
,且 则双曲线
则双曲线 的离心率e等于___________;
的离心率e等于___________;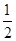 +
+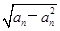 ,且a1=
,且a1=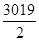
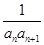 ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.