题目内容
已知双曲线 的左、右焦点分别为
的左、右焦点分别为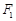 、
、 ,点
,点 在双曲线的右支上,且
在双曲线的右支上,且 ,则
,则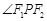 = .
= .

解析试题分析:设 ,
, ,由双曲线定义可得,
,由双曲线定义可得, 在
在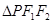 中,
中, =
=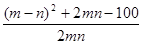

 ,∴
,∴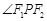 =
= .
.
考点:1、双曲线的标准方程;2、余弦定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知双曲线 的左、右焦点分别为
的左、右焦点分别为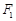 、
、 ,点
,点 在双曲线的右支上,且
在双曲线的右支上,且 ,则
,则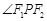 = .
= .

解析试题分析:设 ,
, ,由双曲线定义可得,
,由双曲线定义可得, 在
在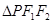 中,
中, =
=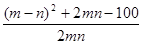

 ,∴
,∴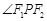 =
= .
.
考点:1、双曲线的标准方程;2、余弦定理.

 阅读快车系列答案
阅读快车系列答案