题目内容
已知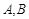 是椭圆
是椭圆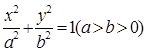 和双曲线
和双曲线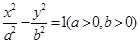 的公共顶点。
的公共顶点。 是双曲线上的动点,
是双曲线上的动点,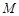 是椭圆上的动点(
是椭圆上的动点(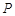 、
、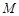 都异于
都异于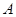 、
、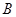 ),且满足
),且满足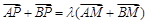 ,其中
,其中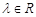 ,设直线
,设直线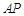 、
、 、
、 、
、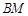 的斜率分别记为
的斜率分别记为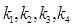 ,
, 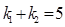 ,则
,则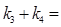
-5
解析试题分析:设出点P、M的坐标,代入双曲线和椭圆的方程,再利用已知满足 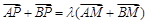
及其斜率的计算公式即可求出.解:∵A,B是椭圆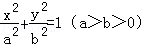 和双曲线
和双曲线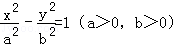 的公共顶点,∴(不妨设)A(﹣a,0),B(a,0).
的公共顶点,∴(不妨设)A(﹣a,0),B(a,0).
设P(x1,y1),M(x2,y2),∵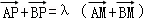 ,其中λ∈R,∴(x1+a,y1)+(x1﹣a,y1)=λ[(x2+a,y2)+(x2﹣a,y2)],化为x1y2=x2y1.
,其中λ∈R,∴(x1+a,y1)+(x1﹣a,y1)=λ[(x2+a,y2)+(x2﹣a,y2)],化为x1y2=x2y1.
∵P、M都异于A、B,∴y1≠0,y2≠0.∴ .
.
由k1+k2=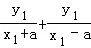 =5,化为
=5,化为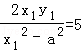 ,(*)
,(*)
又∵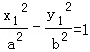 ,∴
,∴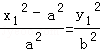 ,代入(*)化为
,代入(*)化为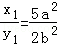 .
.
k3+k4=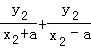 =
=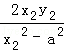 ,又
,又 ,
,
∴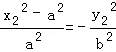 ,
,
∴k3+k4=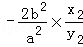 =
=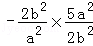 =﹣5.
=﹣5.
故答案为﹣5.
考点:双曲线和椭圆的方程
点评:熟练掌握点在曲线上的意义、双曲线和椭圆的方程、向量的运算性质、斜率的计算公式是解题的关键,同时本题需要较强的计算能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为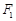 、
、 ,点
,点 在双曲线的右支上,且
在双曲线的右支上,且 ,则
,则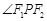 = .
= .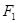 、
、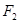 是双曲线
是双曲线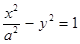 的两个焦点,点
的两个焦点,点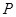 在此双曲线上,
在此双曲线上,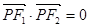 ,如果点
,如果点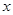 轴的距离等于
轴的距离等于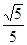 ,那么该双曲线的离心率等于 .
,那么该双曲线的离心率等于 . 是双曲线
是双曲线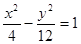 的左焦点,
的左焦点,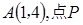 是双曲线右支上的动点,则
是双曲线右支上的动点,则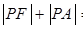 的最小值为 .
的最小值为 .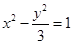 的右焦点
的右焦点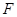 ,点
,点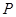 是渐近线上的点,且
是渐近线上的点,且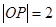 ,则
,则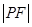 = .
= .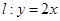 上一点
上一点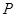 作圆
作圆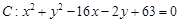 的切线
的切线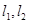 ,若
,若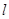 对称,则点
对称,则点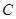 的距离为 .
的距离为 .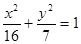 的左右焦点分别为
的左右焦点分别为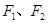 ,过焦点
,过焦点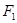 的直线交椭圆于
的直线交椭圆于 两点,若
两点,若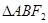 的内切圆的面积为
的内切圆的面积为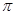 ,设
,设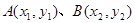 ,则
,则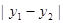 值为 .
值为 .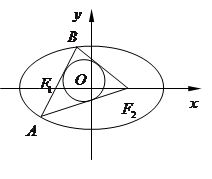
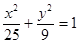 的两个焦点,过F1的直线交椭圆于A、B两点,若
的两个焦点,过F1的直线交椭圆于A、B两点,若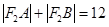 ,则
,则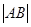 = _____________
= _____________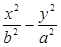 =1的两条渐近线互相垂直,那么该双曲线的离心率是 .
=1的两条渐近线互相垂直,那么该双曲线的离心率是 .