题目内容
【题目】已知函数![]() 的图像在点
的图像在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求实数![]() 的值及函数
的值及函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,比较
时,比较![]() 与
与![]() (
(![]() 为自然对数的底数)的大小.
为自然对数的底数)的大小.
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() 在
在![]() 上得
上得![]() 及
及![]() 得
得![]() 的值,得
的值,得![]() 的解析式,由
的解析式,由![]() 得
得![]() 的增区间,由
的增区间,由![]() 得
得![]() 的减区间;(2)利用函数的单调性结合其图象可知:若
的减区间;(2)利用函数的单调性结合其图象可知:若![]() ,则必有一个小于
,则必有一个小于![]() ,一个大于
,一个大于![]() ,不妨设
,不妨设![]() ,当
,当![]() 时,结论显然成立,当
时,结论显然成立,当![]() 时,
时, ![]() ,令
,令![]() ,对函数求导,可得
,对函数求导,可得![]() 即
即![]() 在
在![]() 单调递增,故
单调递增,故![]() ,得
,得![]() ,结合函数单调性可得结果。
,结合函数单调性可得结果。
(1)函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
因为![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,
,
所以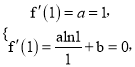 解得
解得![]() ,所以
,所以![]() .
.
所以![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减.
单调递减.
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)当![]() 时,
时, ![]() .证明如下:
.证明如下:
因为![]() 时,
时, ![]() 单调递减,且
单调递减,且![]() ,
,
又![]() ,当
,当![]() 时,
时, ![]() 单调递增,且
单调递增,且![]() .
.
若![]() ,则
,则![]() 必都大于
必都大于![]() ,且必有一个小于
,且必有一个小于![]() ,一个大于
,一个大于![]() .
.
不妨设![]() ,当
,当![]() 时,必有
时,必有![]() .
.
当![]() 时,
时, ![]() ,
,
设![]() ,
,
则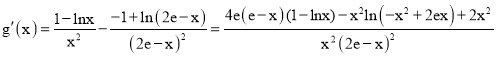
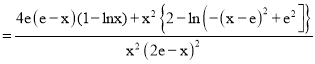
因为![]() ,所以
,所以![]() ,故
,故![]() .
.
又![]() ,所以
,所以![]() ,所以
,所以![]() 在区间
在区间![]() 内单调递增,
内单调递增,
所以![]() ,所以
,所以![]() .
.
因为![]() ,
, ![]() ,所以
,所以![]() ,
,
又因为![]() 在区间
在区间![]() 内单调递增,
内单调递增,
所以![]() ,即
,即![]() .
.
综上,当![]() 时,
时,![]() .
.

练习册系列答案
相关题目
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
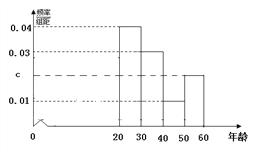
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.