题目内容
【题目】已知f(x)=sin(x﹣30°)+cos(x﹣60°),g(x)=2sin2 ![]() .
.
(1)若α为第一象限角且f(α)= ![]() ,求g(α)之值;
,求g(α)之值;
(2)求f(x﹣1080°)≥g(x)在[0,360°]内的解集.
【答案】
(1)解:∵f(x)=sin(x﹣30°)+cos(x﹣60°)= ![]() sinx﹣
sinx﹣ ![]() cosx+
cosx+ ![]() cosx+
cosx+ ![]() sinx=
sinx= ![]() sinx,
sinx,
g(x)=2sin2 ![]() =1﹣cosx,
=1﹣cosx,
由f(α)= ![]() ,可得:sinα=
,可得:sinα= ![]() ,
,
又α为第一象限角,
∴cos ![]() ,
,
∴g(α)= ![]()
(2)解:由(1)可得f(x)= ![]() sinx,
sinx,
∴f(x﹣1080°)= ![]() sin(x﹣1080°)=
sin(x﹣1080°)= ![]() sinx,
sinx,
∴f(x﹣1080°)≥g(x)等价于 ![]() sinx≥1﹣cosx,即:
sinx≥1﹣cosx,即: ![]() sinx+cosx≥1,
sinx+cosx≥1,
可得:2sin(x+30°)≥1,
∴sin(x+30°)≥ ![]() ,
,
∴k360°+30°≤x+30°≤k360°+150°(k∈Z),
又∵x∈[0°,360°],
∴0°≤x≤120°,
∴f(x﹣1080°)≥g(x)的解集为:[0°,120°]
【解析】(1)利用三角函数恒等变换的应用化简可得f(x)= ![]() sinx,g(x)=1﹣cosx,由f(α)=
sinx,g(x)=1﹣cosx,由f(α)= ![]() ,可求sinα,利用同角三角函数基本关系式可求cosα,进而可求g(α).(2)由(1)利用诱导公式可求f(x﹣1080°)=
,可求sinα,利用同角三角函数基本关系式可求cosα,进而可求g(α).(2)由(1)利用诱导公式可求f(x﹣1080°)= ![]() sinx,由f(x﹣1080°)≥g(x),可得sin(x+30°)≥
sinx,由f(x﹣1080°)≥g(x),可得sin(x+30°)≥ ![]() ,结合范围x∈[0°,360°],利用正弦函数的图象和性质即可得解.
,结合范围x∈[0°,360°],利用正弦函数的图象和性质即可得解.

 阅读快车系列答案
阅读快车系列答案【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
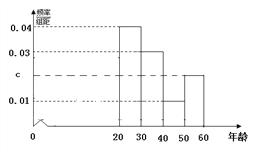
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.