题目内容
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F为棱AD、AB的中点. 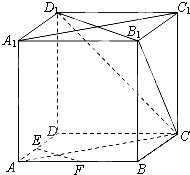
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1 .
【答案】
(1)证明:连接BD.
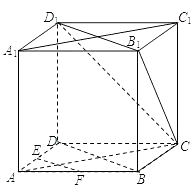
在正方体AC1中,对角线BD∥B1D1.
又因为E、F为棱AD、AB的中点,
所以EF∥BD.
所以EF∥B1D1.
又B1D1平面CB1D1,EF平面CB1D1,
所以EF∥平面CB1D1.
(2)证明:因为在正方体AC1中,
AA1⊥平面A1B1C1D1,而B1D1平面A1B1C1D1,
所以AA1⊥B1D1.
又因为在正方形A1B1C1D1中,A1C1⊥B1D1,
所以B1D1⊥平面CAA1C1.
又因为B1D1平面CB1D1,
所以平面CAA1C1⊥平面CB1D1.
【解析】(1)欲证EF∥平面CB1D1 , 根据直线与平面平行的判定定理可知只需证EF与平面CB1D1内一直线平行,连接BD,根据中位线可知EF∥BD,则EF∥B1D1 , 又B1D1平面CB1D1 , EF平面CB1D1 , 满足定理所需条件;(2)欲证平面CAA1C1⊥平面CB1D1 , 根据面面垂直的判定定理可知在平面CB1D1内一直线与平面CAA1C1垂直,而AA1⊥平面A1B1C1D1 , B1D1平面A1B1C1D1 , 则AA1⊥B1D1 , A1C1⊥B1D1 , 满足线面垂直的判定定理则B1D1⊥平面CAA1C1 , 而B1D1平面CB1D1 , 满足定理所需条件.
【考点精析】关于本题考查的直线与平面平行的判定和平面与平面垂直的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
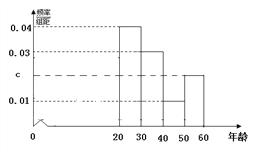
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.