题目内容
【题目】在等差数列{an}中，a1 =-2,a12 =20.
(1)求数列{an}的通项an ；
(2)若bn=
，求数列{
}的前n项和.
【答案】（1）
；（2）
.
【解析】试题分析：（1）先求出公差，再利用等差数列通项公式求解即可；
（2）计算等差数列{an}的前n项和a1+a2+…+an=n(n-3)，得bn=
= n-3，令cn=
=3n-3，利用等比数列求和公式求和即可.
试题解析：
（1）因为an=-2+(n-1)d，所以a12=-2+11d=20，所以d=2，所以
.
（2）因为
，所以a1+a2+…+an=n(n-3)，所以bn=
= n-3.
令cn=
，则cn=3n-3，显然数列{cn}是等比数列，且c1=3-2，公比q=3，
所以数列{
}的前n项和为
．
练习册系列答案
相关题目
【题目】某市为了宣传环保知识，举办了一次“环保知识知多少”的问卷调查活动（一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份， 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
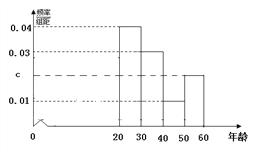
（1）分别求出n， a， b， c的值；
（2）从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”，求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
