题目内容
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,抛物线上一定点
,抛物线上一定点![]() .
.
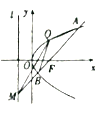
(1)求抛物线![]() 的方程及准线
的方程及准线![]() 的方程;
的方程;
(2)过焦点![]() 的直线(不经过
的直线(不经过![]() 点)与抛物线交于
点)与抛物线交于![]() 两点,与准线
两点,与准线![]() 交于点
交于点![]() ,记
,记![]() 的斜率分别为
的斜率分别为![]() ,问是否存在常数
,问是否存在常数![]() ,使得
,使得![]() 成立?若存在
成立?若存在![]() ,求出
,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】解:(1)![]() ,准线
,准线![]() ;(2)存在常数
;(2)存在常数![]() ,理由见解析.
,理由见解析.
【解析】试题分析:(1)把![]() 代入
代入![]() ,得
,得![]() ,所以抛物线方程为
,所以抛物线方程为![]() ,
,
准线![]() 的方程为
的方程为![]() ;(2)由条件可设直线
;(2)由条件可设直线![]() 的方程为
的方程为![]() .因为
.因为 ![]() ,把直线
,把直线![]() 的方程
的方程![]() ,代入抛物线方程
,代入抛物线方程![]() ,并整理,则
,并整理,则![]() ,因为
,因为![]() 三点共线,所以
三点共线,所以![]() ,
,
所以![]() ,即存在常数
,即存在常数![]() ,使得
,使得![]() 成立.
成立.
试题解析:(1)把![]() 代入
代入![]() ,得
,得![]() ,所以抛物线方程为
,所以抛物线方程为![]() ,
,
准线![]() 的方程为
的方程为![]() .
.
(2)由条件可设直线![]() 的方程为
的方程为![]() .由抛物线准线
.由抛物线准线![]() ,可知
,可知![]() ,又
,又![]() ,所以
,所以![]() ,
,
把直线![]() 的方程
的方程![]() ,代入抛物线方程
,代入抛物线方程![]() ,并整理,可得
,并整理,可得![]() ,设
,设![]() ,则
,则![]() ,
,
又![]() ,故
,故![]() .因为
.因为![]() 三点共线,所以
三点共线,所以![]() ,
,
即![]() ,
,
所以![]() ,
,
即存在常数![]() ,使得
,使得![]() 成立.
成立.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
【题目】甲参加A,B,C三个科目的学业水平考试,其考试成绩合格的概率如下表,假设三个科目的考试甲是否成绩合格相互独立.
科目A | 科目B | 科目C | |
甲 |
|
|
|
(I)求甲至少有一个科目考试成绩合格的概率;
(Ⅱ)设甲参加考试成绩合格的科目数量为X,求X的分布列和数学期望.