题目内容
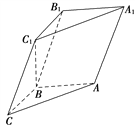
【题目】如图,在三棱柱ABCA1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=![]() .
.
(1)求证:C1B⊥平面ABC;
设![]() (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
试求λ的值.
【答案】(1)见解析(2)1
【解析】试题分析:(1)先由线面垂直的性质证明![]() ,再根据余玄定理及勾股定理证明
,再根据余玄定理及勾股定理证明![]() ,利用直线与平面垂直的判断定理证明
,利用直线与平面垂直的判断定理证明![]() 平面
平面![]() ;(2)通过
;(2)通过![]() 两两垂直.以
两两垂直.以![]() 为原点,
为原点,![]() 所在直线
所在直线![]() 轴建立空间直角坐标系.求出相关点的坐标,求出平面
轴建立空间直角坐标系.求出相关点的坐标,求出平面![]() 的一个法向量,平面BB1E的一个法向量,通过向量的数量积,推出
的一个法向量,平面BB1E的一个法向量,通过向量的数量积,推出![]() 的方程,求解即可.
的方程,求解即可.
试题解析:(1)证明:因为AB⊥侧面BB1C1C,BC1侧面BB1C1C,故AB⊥BC1.
在△BCC1中,BC=1,CC1=BB1=2,∠BCC1=![]() ,
,
BC=BC2+CC-2BC·CC1·cos∠BCC1=12+22-2×1×2×cos![]() =3.
=3.
所以BC1=![]() ,故BC2+BC=CC,所以BC⊥BC1,
,故BC2+BC=CC,所以BC⊥BC1,
而BC∩AB=B 所以C1B⊥平面ABC.
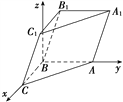
(2)由(1)可知,AB,BC,BC1两两垂直.以B为原点,BC,BA,BC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
则B(0,0,0),A(0,1,0),B1(-1,0,![]() ),C(1,0,0),C1(0,0,
),C(1,0,0),C1(0,0,![]() ).
).
所以=(-1,0,![]() ),所以=(-λ,0,
),所以=(-λ,0,![]() λ
λ![]() λ).
λ).
则=(1-λ,-1,![]() λ),=(-1,-1,
λ),=(-1,-1,![]() ).
).
设平面AB1E的法向量为n=(x,y,z),
则即![]()
令z=![]() ,则x=
,则x=![]() ,y=
,y=![]() ,
,
故n=![]() 是平面AB1E的一个法向量.
是平面AB1E的一个法向量.
因为AB⊥平面BB1C1C,所以=(0,1,0)是平面BB1E的一个法向量,
所以|cos〈n,〉|=
=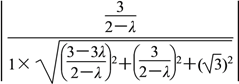
=![]() .
.
两边平方并化简得2λ2-5λ+3=0,所以λ=1或λ=![]() (舍去).
(舍去).
故所求λ的值为1
【方法点晴】本题主要考查线面垂直的判定定理以及利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.

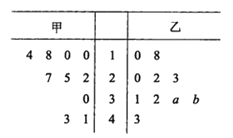
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案