题目内容
如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得PM= PN,试建立适当的坐标系,并求动点P的轨迹方程.
PN,试建立适当的坐标系,并求动点P的轨迹方程.

 PN,试建立适当的坐标系,并求动点P的轨迹方程.
PN,试建立适当的坐标系,并求动点P的轨迹方程.
(x-6)2+y2=33(或x2+y2-12x+3=0).
以O1O2的中点O为原点,O1O2所在的直线为x轴,建立如图所示平面直角坐标系,
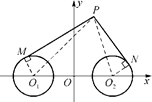
则O1(-2,0),O2(2,0).由已知PM= PN,得PM2=2PN2.因为两圆的半径均为1,所以
PN,得PM2=2PN2.因为两圆的半径均为1,所以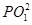 -1=2(
-1=2(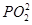 -1).设P(x,y),则(x+2)2+y2-1=2[(x-2)2+y2-1],即(x-6)2+y2=33,
-1).设P(x,y),则(x+2)2+y2-1=2[(x-2)2+y2-1],即(x-6)2+y2=33,
所以所求轨迹方程为(x-6)2+y2=33(或x2+y2-12x+3=0).

则O1(-2,0),O2(2,0).由已知PM=
 PN,得PM2=2PN2.因为两圆的半径均为1,所以
PN,得PM2=2PN2.因为两圆的半径均为1,所以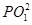 -1=2(
-1=2(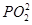 -1).设P(x,y),则(x+2)2+y2-1=2[(x-2)2+y2-1],即(x-6)2+y2=33,
-1).设P(x,y),则(x+2)2+y2-1=2[(x-2)2+y2-1],即(x-6)2+y2=33,所以所求轨迹方程为(x-6)2+y2=33(或x2+y2-12x+3=0).

练习册系列答案
相关题目
 的半径为1,其圆心与点
的半径为1,其圆心与点 关于直线
关于直线 对称,则圆
对称,则圆 ,关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值为
,关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值为  上总存在两个点到原点的距离为
上总存在两个点到原点的距离为 则实数a的取值范围是
则实数a的取值范围是


 到圆
到圆 上的点的距离的最小值是( )
上的点的距离的最小值是( ) 在直线
在直线 上,若圆
上,若圆 (
( 为坐标原点)上存在点
为坐标原点)上存在点 使得
使得 ,则
,则 的取值范围为 .
的取值范围为 .