题目内容
已知圆M过两点A(1，－1)，B(－1，1)，且圆心M在x＋y－2＝0上．
(1)求圆M的方程；
(2)设P是直线3x＋4y＋8＝0上的动点，PA′、PB′是圆M的两条切线，A′、B′为切点，求四边形PA′MB′面积的最小值．
(1)求圆M的方程；
(2)设P是直线3x＋4y＋8＝0上的动点，PA′、PB′是圆M的两条切线，A′、B′为切点，求四边形PA′MB′面积的最小值．
（1）(x－1)2＋(y－1)2＝4.（2）2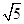
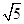
(1)设圆M的方程为(x－a)2＋(y－b)2＝r2
(r>0)，根据题意得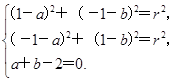
解得a＝b＝1，r＝2.
故所求圆M的方程为(x－1)2＋(y－1)2＝4.
(2)由题知，四边形PA′MB′的面积为S＝S△PA′M＋S△PB′M＝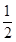
|A′M||PA′|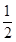＋|B′M||PB′|.又|A′M|＝|B′M|＝2，|PA′|＝|PB′|，所以S＝2|PA′|，而|PA′|＝
＝
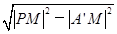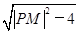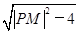，即S＝2.因此要求S的最小值，只需求|PM|的最小值即可，即在直线3x＋4y＋8＝0上找一点P，使得|PM|的值最小，所以|PM|min＝
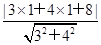＝3，所以四边形PA′MB′面积的最小值为S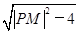＝2＝2
＝2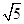
(r>0)，根据题意得
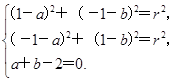解得a＝b＝1，r＝2.故所求圆M的方程为(x－1)2＋(y－1)2＝4.
(2)由题知，四边形PA′MB′的面积为S＝S△PA′M＋S△PB′M＝
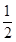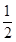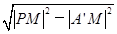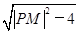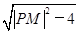|A′M||PA′|＋|B′M||PB′|.又|A′M|＝|B′M|＝2，|PA′|＝|PB′|，所以S＝2|PA′|，而|PA′|＝＝，即S＝2.因此要求S的最小值，只需求|PM|的最小值即可，即在直线3x＋4y＋8＝0上找一点P，使得|PM|的值最小，所以|PM|min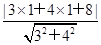＝＝3，所以四边形PA′MB′面积的最小值为S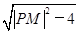＝2＝2＝2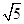
练习册系列答案
相关题目
为圆心的圆经过点
和
，且圆心在直线
上.
在圆
的面积的最大值.
，圆心在直线
：
上，且被直线
：
所截弦的长为
的圆的方程.
PN，试建立适当的坐标系，并求动点P的轨迹方程．
x2-
x+1与x轴正半轴的交点分别为A,B,与y轴正半轴的交点是C,则过A,B,C三点的圆的标准方程是 .