题目内容
已知方程x2＋y2－2(m＋3)x＋2(1－4m2)y＋16m4＋9＝0表示一个圆．
(1)求实数m的取值范围；
(2)求该圆半径r的取值范围；
(3)求圆心的轨迹方程．
(1)求实数m的取值范围；
(2)求该圆半径r的取值范围；
(3)求圆心的轨迹方程．
（1）－
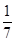<m<1（2）0<r≤
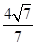（3）y＝4(x－3)2－1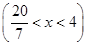
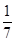<m<1（2）0<r≤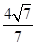（3）y＝4(x－3)2－1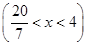(1)方程表示圆的充要条件是D2＋E2－4F>0，即有4(m＋3)2＋4(1－4m2)2－4(16m4＋9)
>0?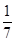－<m<1.
(2)半径r＝
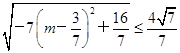?0<r≤.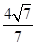
(3)设圆心坐标为(x，y)，则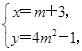
消去m，得y＝4(x－3)2－1.由于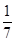－<m<1，
所以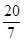
<x<4.故圆心的轨迹方程为y＝4(x－3)2－1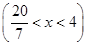
>0?－
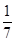<m<1.(2)半径r＝
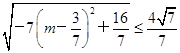?0<r≤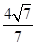.(3)设圆心坐标为(x，y)，则
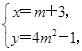消去m，得y＝4(x－3)2－1.由于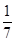－<m<1，所以
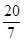<x<4.故圆心的轨迹方程为y＝4(x－3)2－1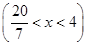
练习册系列答案
相关题目
和原点，则圆的方程为 ；
，求该圆的方程．
PN，试建立适当的坐标系，并求动点P的轨迹方程．
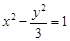的渐近线截得的弦长为
，则圆C的方程为（ ）
)2=
的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径作圆与斜边AB交于点D，则BD的长为 ；