Question

18．设f（x）=asinx+b（a＞0），若f（x）的最大值为$\frac{3}{2}$，最小值为-$\frac{1}{2}$
（1）求f（x）的解析式；
（2）当x∈[0，2π]，作f（x）的图象．

Answer 1

分析 （1）由题意可得a+b=$\frac{3}{2}$，-a+b=-$\frac{1}{2}$，求得a和b的值，可得f（x）的解析式．
（2）当x∈[0，2π]，用五点法作出它的简图．

解答 解：（1）由题意可得a+b=$\frac{3}{2}$，-a+b=-$\frac{1}{2}$，求得a=1，b=$\frac{1}{2}$，
∴f（x）=sinx+$\frac{1}{2}$．
（2）当x∈[0，2π]，列表：

x	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
f（x）	$\frac{1}{2}$	$\frac{3}{2}$	$\frac{1}{2}$	$-\frac{1}{2}$	$\frac{1}{2}$

作图：

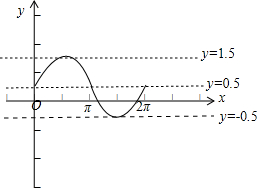
点评 本题主要考查求三角函数的解析式，用五点法作y=Asin（ωx+φ）在一个周期上的简图，属于基础题．