题目内容
19.若△ABC外接圆的圆心为O,半径为4,$\overrightarrow{OA}$+2$\overrightarrow{OB}$+2$\overrightarrow{OC}$=$\overrightarrow{0}$,则$\overrightarrow{CA}$在$\overrightarrow{CB}$上的投影为$\sqrt{15}$.分析 运用向量的平行四边形法则,取BC的中点D,连接OD并延长到点E,使得$\overrightarrow{DE}$=$\overrightarrow{OD}$,则OD⊥BC,且$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{OE}$,再由勾股定理和向量的投影的概念即可求得结果.
解答 解:$\overrightarrow{OA}$+2$\overrightarrow{OB}$+2$\overrightarrow{OC}$=$\overrightarrow{0}$,即为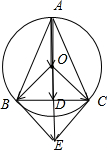
$\overrightarrow{AO}$=2($\overrightarrow{OB}$+$\overrightarrow{OC}$),
取BC的中点D,连接OD并延长到点E,使得$\overrightarrow{DE}$=$\overrightarrow{OD}$,
则OD⊥BC,由于$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{OE}$,
∴$\overrightarrow{AO}$=2$\overrightarrow{OE}$,
由|$\overrightarrow{AO}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=4,
∴|$\overrightarrow{OD}$|=1,
∴CD=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$.
∴向量$\overrightarrow{CA}$在$\overrightarrow{CB}$方向上的投影为$\sqrt{15}$.
故答案为:$\sqrt{15}$.
点评 本题考查了菱形的性质、向量的平行四边形法则、三角形外心的性质、向量的投影、勾股定理、向量共线定理,考查了推理能力与计算能力,属于中档题.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | -e | B. | $\frac{1}{e}$ | C. | e2 | D. | -$\frac{1}{e}$ |