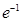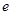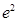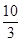题目内容
(1)已知函数f(x)=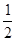 x
x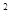 -ax+(a-1)
-ax+(a-1)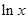 ,
,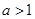 。讨论函数
。讨论函数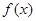 的单调性;
的单调性;
(2).已知函数f (x)=lnx,g(x)=ex.设直线l为函数 y=f (x) 的图象上一点A(x0,f (x0))处的切线.问在区间(1,+∞)上是否存在x0,使得直线l与曲线y=g(x)也相切.若存在,这样的x0有几个?,若没有,则说明理由。
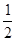 x
x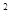 -ax+(a-1)
-ax+(a-1)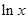 ,
,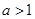 。讨论函数
。讨论函数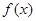 的单调性;
的单调性; (2).已知函数f (x)=lnx,g(x)=ex.设直线l为函数 y=f (x) 的图象上一点A(x0,f (x0))处的切线.问在区间(1,+∞)上是否存在x0,使得直线l与曲线y=g(x)也相切.若存在,这样的x0有几个?,若没有,则说明理由。
(1)当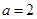 时,
时,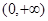 递增
递增
当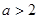 时,在(0,1),
时,在(0,1),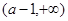 递增 在(1,a-1)递减
递增 在(1,a-1)递减
当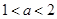 时,在(0,a-1)递增,
时,在(0,a-1)递增,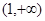 递增,在(a-1,1)递减
递增,在(a-1,1)递减
(2)在区间(1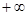 )一定存在唯一的
)一定存在唯一的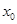 ,使直线l与曲线
,使直线l与曲线 也相切.
也相切.
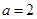 时,
时,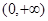 递增
递增当
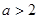 时,在(0,1),
时,在(0,1),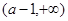 递增 在(1,a-1)递减
递增 在(1,a-1)递减当
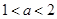 时,在(0,a-1)递增,
时,在(0,a-1)递增,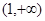 递增,在(a-1,1)递减
递增,在(a-1,1)递减(2)在区间(1
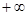 )一定存在唯一的
)一定存在唯一的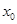 ,使直线l与曲线
,使直线l与曲线 也相切.
也相切.第一问中,利用f(x)=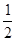 x
x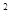 -ax+(a-1)
-ax+(a-1)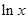 ,
, 求解导数,然后对于参数a分情况讨论可知函数的单调性。
求解导数,然后对于参数a分情况讨论可知函数的单调性。
第二问中,利用导数的几何意义,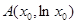
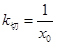
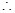 切线l的方程为:
切线l的方程为: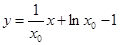
设切线l与曲线 相切于
相切于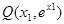
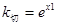 切线l的方程又为
切线l的方程又为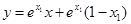
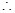
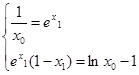
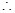
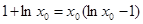
因为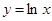 与
与
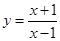 的图象 在(1,
的图象 在(1,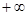 )
)
有且只有一个交点
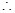 在区间(1
在区间(1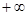 )一定存在唯一的
)一定存在唯一的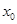 ,使直线l与曲线
,使直线l与曲线 也相切
也相切
解:(1)当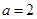 时,
时,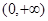 递增
递增
当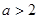 时,在(0,1),
时,在(0,1),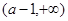 递增 在(1,a-1)递减
递增 在(1,a-1)递减
当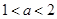 时,在(0,a-1)递增,
时,在(0,a-1)递增,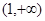 递增,在(a-1,1)递减………7分
递增,在(a-1,1)递减………7分
(2)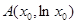
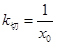
 切线l的方程为:
切线l的方程为: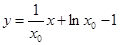
设切线l与曲线 相切于
相切于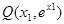
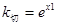 切线l的方程又为
切线l的方程又为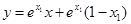
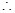
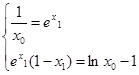
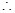
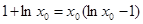
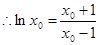 ………7分
………7分
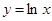 与
与
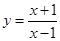 的图象 在(1,
的图象 在(1,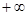 )
)
有且只有一个交点
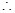 在区间(1
在区间(1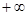 )一定存在唯一的
)一定存在唯一的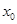 ,使直线l与曲线
,使直线l与曲线 也相切…………………15分
也相切…………………15分
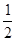 x
x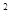 -ax+(a-1)
-ax+(a-1)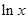 ,
,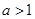 求解导数,然后对于参数a分情况讨论可知函数的单调性。
求解导数,然后对于参数a分情况讨论可知函数的单调性。第二问中,利用导数的几何意义,
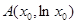
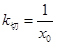
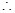 切线l的方程为:
切线l的方程为: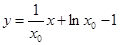
设切线l与曲线
 相切于
相切于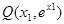
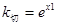 切线l的方程又为
切线l的方程又为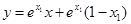
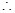
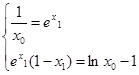
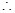
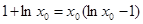
因为
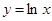 与
与
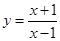 的图象 在(1,
的图象 在(1,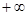 )
)有且只有一个交点
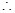 在区间(1
在区间(1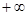 )一定存在唯一的
)一定存在唯一的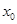 ,使直线l与曲线
,使直线l与曲线 也相切
也相切解:(1)当
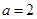 时,
时,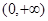 递增
递增当
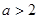 时,在(0,1),
时,在(0,1),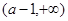 递增 在(1,a-1)递减
递增 在(1,a-1)递减当
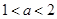 时,在(0,a-1)递增,
时,在(0,a-1)递增,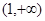 递增,在(a-1,1)递减………7分
递增,在(a-1,1)递减………7分(2)
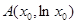
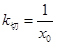
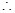 切线l的方程为:
切线l的方程为: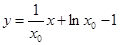
设切线l与曲线
 相切于
相切于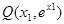
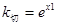 切线l的方程又为
切线l的方程又为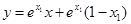
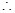
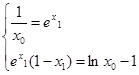
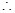
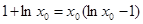
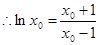 ………7分
………7分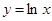 与
与
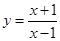 的图象 在(1,
的图象 在(1,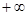 )
)有且只有一个交点
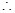 在区间(1
在区间(1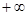 )一定存在唯一的
)一定存在唯一的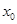 ,使直线l与曲线
,使直线l与曲线 也相切…………………15分
也相切…………………15分
练习册系列答案
相关题目
 在
在 和
和 处取得极值,
处取得极值, 的值;
的值; 在
在 上的最大值和最小值.
上的最大值和最小值. ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
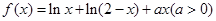 .
.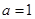 时,求
时,求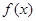 的单调区间;
的单调区间;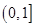 上的最大值为
上的最大值为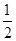 ,求
,求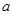 的值.
的值.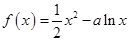 (
(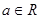 )
)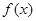 的图象在
的图象在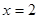 处的切线方程为
处的切线方程为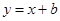 ,求
,求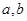 的值;
的值;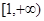 为增函数,求
为增函数,求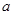 的取值范围.
的取值范围.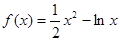 的单调增区间为 .
的单调增区间为 .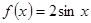 (
(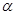 为常数),则
为常数),则 ( )
( )
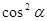

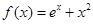 ,则
,则 .
.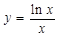 的最大值为( )
的最大值为( )