题目内容
若函数 在
在 和
和 处取得极值,
处取得极值,
(1)求 的值;
的值;
(2)求 在
在 上的最大值和最小值.
上的最大值和最小值.
 在
在 和
和 处取得极值,
处取得极值,(1)求
 的值;
的值;(2)求
 在
在 上的最大值和最小值.
上的最大值和最小值.(1)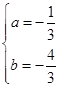 (2)最大值为
(2)最大值为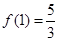 ,最小值为
,最小值为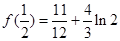
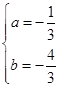 (2)最大值为
(2)最大值为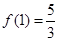 ,最小值为
,最小值为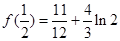
(1)先求出导函数,然后利用极值的性质求出参数a和b;(2)先用导数法求出函数在给定区间内的单调区间,然后利用单调性求出函数的最值
1)由题意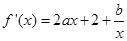 , 由
, 由 在
在 和
和 处取得极值得
处取得极值得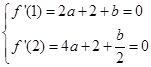 解得
解得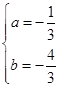 ……7分
……7分
(2)由(1)知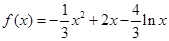 ,故
,故
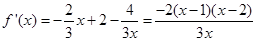 由
由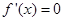 得
得 或
或
在 上当
上当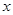 变化时,
变化时,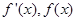 变化情况列表得
变化情况列表得
所以,当 时,
时, 取得极大值
取得极大值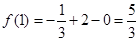
又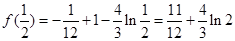 ,
,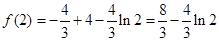
所以 在
在 上的最大值为
上的最大值为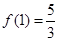 ,最小值为
,最小值为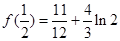
1)由题意
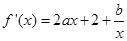 , 由
, 由 在
在 和
和 处取得极值得
处取得极值得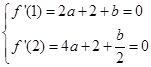 解得
解得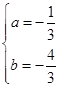 ……7分
……7分(2)由(1)知
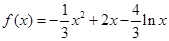 ,故
,故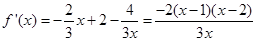 由
由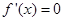 得
得 或
或
在
 上当
上当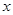 变化时,
变化时,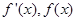 变化情况列表得
变化情况列表得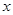 | 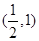 | 1 | 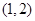 |
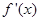 | — | 0 | + |
 | 单调递减 | 极大值 | 单调递增 |
 时,
时, 取得极大值
取得极大值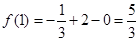
又
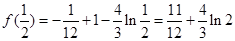 ,
,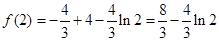
所以
 在
在 上的最大值为
上的最大值为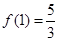 ,最小值为
,最小值为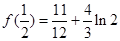

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
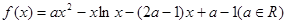 .
.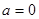 时,求函数
时,求函数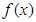 在点
在点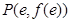 处的切线方程;
处的切线方程;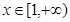 函数
函数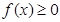 恒成立,求实数
恒成立,求实数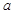 的取值范围.
的取值范围.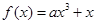 在定义域
在定义域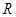 上恰有三个单调区间,则
上恰有三个单调区间,则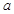 的取值范围是( )
的取值范围是( )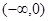
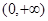
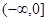
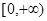
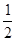 x
x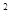 -ax+(a-1)
-ax+(a-1)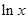 ,
,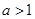 。讨论函数
。讨论函数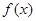 的单调性;
的单调性; 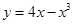 在点
在点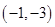 处的切线方程是____________
处的切线方程是____________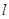 与函数f(x)=x3图像相切,且
与函数f(x)=x3图像相切,且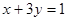 垂直,则直线
垂直,则直线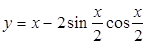 ,则
,则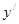 =
= 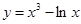 在点(1,2)处的切线方程为
在点(1,2)处的切线方程为 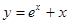 在点(0,1)处的切线方程为
在点(0,1)处的切线方程为


