题目内容
20.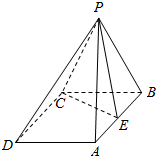 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.(1)求证:PE⊥AD;
(2)若∠ADC=$\frac{π}{3}$,求证:平面PEC⊥平面PAB.
分析 (1)由等腰三角形的性质和面面垂直的性质定理,可得PE⊥平面ABCD,再由线面垂直的性质,即可得证;
(2)由线面垂直的判定定理可得AB⊥平面PEC,再由面面垂直的判定定理即可得证.
解答 证明:(1)因为PA=PB,点E是棱AB的中点,
所以PE⊥AB,
因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PE?平面PAB,
所以PE⊥平面ABCD,
因为AD?平面ABCD,
所以PE⊥AD;
(2)依题意,有CA=CB,点E是棱AB的中点,
所以CE⊥AB,
由(1)可得PE⊥AB,
所以AB⊥平面PEC,
又因为AB?平面PAB,
所以平面PAB⊥平面PEC.
点评 本题考查空间线面垂直和面面垂直的判定和性质的运用,考查空间想象能力和逻辑推理能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知函数y=$\sqrt{m{x^2}+6mx+m+8}$的定义域为R,求实数m的取值范围是( )
| A. | [0,1] | B. | (0,1) | C. | (0,2) | D. | [0,2] |