题目内容
10.(1)若f(x)+f($\frac{x-1}{x}$)=1+x,求f(x);(2)若2f(x)+f(1-x)=1+x,求f(x).
分析 (1)利用换元法以及方程组求解函数的解析式.
(2)用1-x代替式中的x可得方程,和已知式子联立解方程组可得.
解答 解:(1)f(x)+f($\frac{x-1}{x}$)=1+x,可得f(x)+f(1-$\frac{1}{x}$)=1+x…①,
用1-$\frac{1}{x}$换x可得:f(1-$\frac{1}{x}$)+f($\frac{1-\frac{1}{x}-1}{1-\frac{1}{x}}$)=-$\frac{1}{x}$,即f(1-$\frac{1}{x}$)+f($\frac{1}{1-x}$)=-$\frac{1}{x}$,…②,
利用$\frac{1}{1-x}$换f(x)+f(1-$\frac{1}{x}$)=1+x 中的x可得:f($\frac{1}{1-x}$)+f($1-\frac{1}{\frac{1}{1-x}}$)=1+$\frac{1}{1-x}$,即f($\frac{1}{1-x}$)+f(x)=1+$\frac{1}{1-x}$…③,
①-②+③可得:2f(x)=1+x+$\frac{1}{x}$+1+$\frac{1}{1-x}$,
解得f(x)=1+$\frac{x}{2}$$+\frac{1}{2x}$+$\frac{1}{2-2x}$.
(2)∵2f(x)+f(1-x)=1+x,
∴用1-x代替式中的x可得2f(1-x)+f(x)=2-x,
两式联立消去f(1-x)可得3f(x)=3x,
所求函数的解析式为:f(x)=x.
点评 本题考查函数解析式的求解方法,涉及方程组的思想,属基础题.

练习册系列答案
相关题目
18.若一元二次不等式x2-$\frac{2}{\sqrt{a}}$x+1-$\frac{1}{b}$>0(b>a)的解集为{x|x≠$\frac{1}{\sqrt{a}}$},则$\frac{4}{a-1}$+$\frac{16}{b-1}$的最小值为( )
| A. | 16 | B. | 25 | C. | 36 | D. | 49 |
4.如图,直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=( )
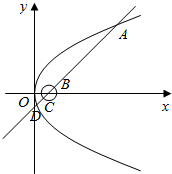

| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
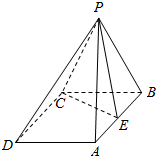 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.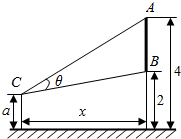 如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.
如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.