题目内容
5.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,一条准线方程为x=3,求椭圆C的标准方程.分析 根据离心率和准线方程求得a和c,则b可得,则椭圆的方程可得.
解答 解:∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,一条准线方程为x=3,
∴e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,$\frac{{a}^{2}}{c}$=3,
∴a=$\sqrt{3}$,c=1,
∴b=$\sqrt{2}$,
∴椭圆的方程为:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}$=1.
点评 本题主要考查了椭圆的标准方程,椭圆的简单性质.考查了学生分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.设f(x)是(x2+$\frac{1}{2x}$)6展开式的中间项,若存在x∈[$\frac{\sqrt{2}}{2}$,$\sqrt{2}$]使f(x)≤mx成立,则实数m的取值范围是( )
| A. | (-∞,$\frac{5}{4}$) | B. | (-∞,$\frac{5}{4}$] | C. | ($\frac{5}{4}$,+∞) | D. | [$\frac{5}{4}$,+∞) |
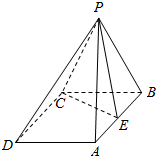 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.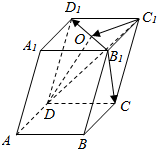 如图,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:B1C∥平面ODC1.
如图,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:B1C∥平面ODC1.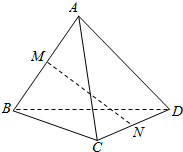 如图,空间四边形ABCD的每条边和AC,BD的长都等于a,点M,N分别是AB,CD的中点,求证:MN⊥AB,MN⊥CD.
如图,空间四边形ABCD的每条边和AC,BD的长都等于a,点M,N分别是AB,CD的中点,求证:MN⊥AB,MN⊥CD.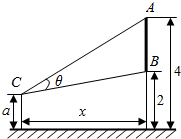 如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.
如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.