题目内容
8.已知O是△ABC所在平面内一点.(1)已知D为BC边中点,且2$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,证明:$\overrightarrow{AO}=\overrightarrow{OD.}$;
(2)已知$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}$=$\overrightarrow{0}$,△BOC的面积为2,求△ABC的面积.
分析 (1)如图所示,以OB,OC为邻边作平行四边形OBEC,可得$\overrightarrow{OB}+\overrightarrow{OC}$=$\overrightarrow{OE}=2\overrightarrow{OD}$,已知2$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,可得$2\overrightarrow{OA}+2\overrightarrow{OD}$=$\overrightarrow{0}$,即可证明.
(2)如图所示,作OD=2OB,OE=3OC,可得$\overrightarrow{OA}+\overline{OD}+\overline{OE}$=$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}$=$\overrightarrow{0}$,可得点O是△ADC的重心.由于△BOC的面积为2,可得$\frac{{S}_{△BOC}}{{S}_{△ODC}}$=$\frac{OB•OC}{OD•OE}$=$\frac{1}{6}$=$\frac{2}{{S}_{△ODC}}$,可得S△ODC=12,同理可得S△OAE=S△OAD=12,即可得出.
解答 (1)证明:如图所示,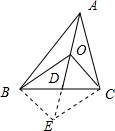
以OB,OC为邻边作平行四边形OBEC,
则$\overrightarrow{OB}+\overrightarrow{OC}$=$\overrightarrow{OE}=2\overrightarrow{OD}$,
∵2$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,
∴$2\overrightarrow{OA}+2\overrightarrow{OD}$=$\overrightarrow{0}$,
∴$\overrightarrow{AO}=\overrightarrow{OD.}$
(2)解:如图所示,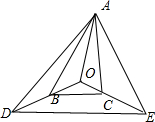
作OD=2OB,OE=3OC,
则$\overrightarrow{OA}+\overline{OD}+\overline{OE}$=$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}$=$\overrightarrow{0}$,
∴点O是△ADC的重心.
∵△BOC的面积为2,
∴$\frac{{S}_{△BOC}}{{S}_{△ODC}}$=$\frac{OB•OC}{OD•OE}$=$\frac{1}{2}×\frac{1}{3}$=$\frac{1}{6}$=$\frac{2}{{S}_{△ODC}}$,可得S△ODC=12,
同理可得S△OAE=S△OAD=12,
可得S△OAC=$\frac{1}{3}$S△OAE=4,S△OAB=$\frac{1}{2}{S}_{△OAD}$=6,
∴S△ABC=S△OBC+S△OAC+S△OAB=2+4+6=12.
点评 本题考查了向量的平行四边形法则、三角形的重心性质、三角形的面积计算,考查了推理能力与计算能力,属于中档题.

| A. | 10个教职工中,必有1人当选 | |
| B. | 每位教职工当选的可能性是$\frac{1}{10}$ | |
| C. | 数学教研组共有50人,该组当选教工代表的人数一定是5 | |
| D. | 以上说法都不正确 |
| A. | A?B | B. | B?A | C. | A=B | D. | A∩B=Φ |
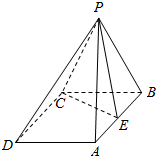 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.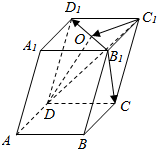 如图,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:B1C∥平面ODC1.
如图,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:B1C∥平面ODC1.