Question

【题目】函数f（x）=x2+ax+3．
（1）当x∈R时，f（x）≥a恒成立，求a的取值范围．
（2）当x∈[﹣2，2]时，f（x）≥a恒成立，求a的取值范围．

Answer 1

【答案】
（1）解：∵x∈R时，有x2+ax+3﹣a≥0恒成立，

须△=a2﹣4（3﹣a）≤0，即a2+4a﹣12≤0，所以﹣6≤a≤2

（2）解：当x∈[﹣2，2]时，设g（x）=x2+ax+3﹣a≥0，

分如下三种情况讨论（如图所示）：

①如图（1），当g（x）的图象恒在x轴上方时，满足条件时，有△=a2﹣4（3﹣a）≤0，即﹣6≤a≤2．

②如图（2），g（x）的图象与x轴有交点，

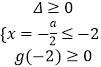当﹣ ≤﹣2时，g（x）≥0，即 即 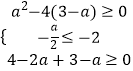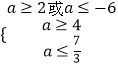解之得a∈Φ．

③如图（3），g（x）的图象与x轴有交点，

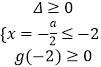﹣ ≥﹣2时，g（x）≥0，即 即 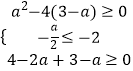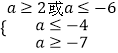﹣7≤a≤﹣6

综合①②③得a∈[﹣7，2]．

【解析】（1）对一切实数x恒成立，转化为二次函数恒为非负，利用根的判别式小于等于0即可．（2）对于[﹣2，2]区间内的任意x恒成立，同样考虑二次函数的最值问题，按区间与对称轴的关系分三种情况讨，最后结合图象即可解决问题．
【考点精析】本题主要考查了解一元二次不等式的相关知识点，需要掌握求一元二次不等式解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边才能正确解答此题．