ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄżËæŚĆÊÖ»ú”Ä·ąŐ裏Ą°ÎąĐĆĄ±ÔœÀŽÔœłÉÎȘÈËĂÇœ»Áś”ÄÒ»ÖÖ·œÊœ.Äł»účč¶ÔĄ°ÊčÓĂÎąĐĆœ»ÁśĄ±”ÄÌŹ¶ÈœűĐĐ”śČ飏Ëæ»úłéÈĄÁË50ÈËŁŹËûĂÇÄêÁä”ÄÆ”Êę·ÖČŒŒ°¶ÔĄ°ÊčÓĂÎąĐĆœ»ÁśĄ±ÔȚłÉÈËÊęÈçϱí.
ÄêÁ䣚”„λŁșËêŁ© | [15,25Ł© | [25,35Ł© | [35,45Ł© | [45,55Ł© | [55,65Ł© | [65,75Ł© |
Æ”Êę | 5 | 10 | 15 | 10 | 5 | 5 |
ÔȚłÉÈËÊę | 5 | 10 | 12 | 7 | 2 | 1 |
ŁšąńŁ©ÈôÒÔĄ°ÄêÁä45ËêÎȘ·Öœç”㥱ŁŹÓÉÒÔÉÏÍłŒÆÊęŸĘÍêłÉÏÂĂæ![]() ÁĐÁȘ±íŁŹČąĆжÏÊÇ·ńÓĐ99%”Ä°ŃÎŐÈÏÎȘĄ°ÊčÓĂÎąĐĆœ»ÁśĄ±”ÄÌŹ¶ÈÓëÈË”ÄÄêÁäÓĐčŰŁ»
ÁĐÁȘ±íŁŹČąĆжÏÊÇ·ńÓĐ99%”Ä°ŃÎŐÈÏÎȘĄ°ÊčÓĂÎąĐĆœ»ÁśĄ±”ÄÌŹ¶ÈÓëÈË”ÄÄêÁäÓĐčŰŁ»
ÄêÁäČ»”ÍÓÚ45Ëê”ÄÈËÊę | ÄêÁä”ÍÓÚ45Ëê”ÄÈËÊę | șÏŒÆ | |
ÔȚłÉ | |||
Č»ÔȚłÉ | |||
șÏŒÆ |
ŁšąòŁ©ÈôŽÓÄêÁäÔÚ[25,35Ł©șÍ[55,65Ł©”ı»”śČéÈËÖĐ°ŽŐŐ·ÖČăłéŃù”Ä·œ·šŃĄÈĄ6ÈËœűĐĐŚ·ŚÙ”śČ飏ȹžűÓèÆäÖĐ3ÈËĄ°șì°üĄ±œ±ÀűŁŹÇó3ÈËÖĐÖÁÉÙÓĐ1ÈËÄêÁäÔÚ[55,65Ł©”ÄžĆÂÊ.
ČÎżŒÊęŸĘÈçÏÂŁș
žœÁÙœçÖ”±íŁș
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ”ÄčÛČâÖ”Łș
”ÄčÛČâÖ”Łș ![]() ŁšÆäÖĐ
ŁšÆäÖĐ![]() Ł©
Ł©
ĄŸŽđ°žĄżŁšąńŁ©ÁĐÁȘ±íŒûœâÎöŁŹÓĐ![]() ”Ä°ŃÎŐÈÏÎȘĄ°ÊčÓĂÎąĐĆœ»ÁśĄ±”ÄÌŹ¶ÈÓëÈË”ÄÄêÁäÓĐčŰŁ»ŁšąòŁ©
”Ä°ŃÎŐÈÏÎȘĄ°ÊčÓĂÎąĐĆœ»ÁśĄ±”ÄÌŹ¶ÈÓëÈË”ÄÄêÁäÓĐčŰŁ»ŁšąòŁ©![]() Łź
Łź
ĄŸœâÎöĄżÊÔÌâ·ÖÎöŁș
ŁšąńŁ©ÓÉËùžűÊęŸĘżÉÒÔŒÆËăłöÄêÁäČ»”ÍÓÚ45ËêșÍÄêÁä”ÍÓÚ45Ëê”Ä”ÄÈËÖĐÔȚłÉĄąČ»ÔȚłÉ”ÄÈËÊ꣏ŽÓ¶űżÉ”ĂÁĐÁȘ±íŁŹÔÙÓÉËùžűč«ÊœŒÆËă![]() żÉÖȘÓĐÎȚ°ŃÎŐŁ»
żÉÖȘÓĐÎȚ°ŃÎŐŁ»
ŁšąòŁ©ÓÉ·ÖČăłéŃùÖȘÇűŒä![]() ÉÏÓĐ2ÈËŁŹÇűŒä
ÉÏÓĐ2ÈËŁŹÇűŒä![]() ÉÏÓĐ4ÈËŁŹ°ŃŐâ6ÈË·Ö±đ±àșĆșóŁŹżÉÁĐŸÙłöÈÎÈĄ3È˔ĞśÖÖŚéșÏŁŹ·Ö±đŒÆËășóżÉ”ĂËùÇóžĆÂÊŁź
ÉÏÓĐ4ÈËŁŹ°ŃŐâ6ÈË·Ö±đ±àșĆșóŁŹżÉÁĐŸÙłöÈÎÈĄ3È˔ĞśÖÖŚéșÏŁŹ·Ö±đŒÆËășóżÉ”ĂËùÇóžĆÂÊŁź
ÊÔÌâœâÎöŁș
ŁšąńŁ©žùŸĘÌőŒț”Ă![]() ÁĐÁȘ±íŁș
ÁĐÁȘ±íŁș
ÄêÁäČ»”ÍÓÚ45Ëê”ÄÈËÊę | ÄêÁä”ÍÓÚ45Ëê”ÄÈËÊę | șÏŒÆ | |
ÔȚłÉ | 10 | 27 | 37 |
Č»ÔȚłÉ | 10 | 3 | 13 |
șÏŒÆ | 20 | 30 | 50 |
žùŸĘÁĐÁȘ±íËùžű”ÄÊęŸĘŽúÈëč«Êœ”Ă”œŁș
![]()
ËùÒÔÓĐ![]() ”Ä°ŃÎŐÈÏÎȘĄ°ÊčÓĂÎąĐĆœ»ÁśĄ±”ÄÌŹ¶ÈÓëÈË”ÄÄêÁäÓĐčŰ;
”Ä°ŃÎŐÈÏÎȘĄ°ÊčÓĂÎąĐĆœ»ÁśĄ±”ÄÌŹ¶ÈÓëÈË”ÄÄêÁäÓĐčŰ;
ŁšąòŁ©œâŁș
°ŽŐŐ·ÖČăłéŃù·œ·šżÉÖȘŁș
[55,65Ł©ŁšËêŁ©łéÈĄŁș![]() ŁšÈËŁ©Ł»
ŁšÈËŁ©Ł»
[25,35Ł©ŁšËêŁ©łéÈĄŁș![]() ŁšÈËŁ©
ŁšÈËŁ©
œâŁșÔÚÉÏÊöłéÈĄ”Ä6ÈËÖĐ, ÄêÁäÔÚ[55,65Ł©ŁšËêŁ©ÓĐ2ÈËŁŹÄêÁä[25,35Ł©ŁšËêŁ©ÓĐ4ÈËĄŁ
ÄêÁäÔÚ[55,65Ł©ŁšËêŁ©ŒÇÎȘ![]() Ł»ÄêÁäÔÚ[25,35Ł©ŁšËêŁ©ŒÇÎȘ
Ł»ÄêÁäÔÚ[25,35Ł©ŁšËêŁ©ŒÇÎȘ![]() ŁŹ ÔòŽÓ6ÈËÖĐÈÎÈĄ3Ăû”ÄËùÓĐÇéżöÎȘ:
ŁŹ ÔòŽÓ6ÈËÖĐÈÎÈĄ3Ăû”ÄËùÓĐÇéżöÎȘ: ![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]()
![]()
![]()
![]() čČ20ÖÖÇéżöŁŹ
čČ20ÖÖÇéżöŁŹ
ÆäÖĐÖÁÉÙÓĐÒ»ÈËÄêÁäÔÚ[55,65Ł©ËêÇéżöÓĐŁș![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() ŁŹčČ16ÖÖÇéżöĄŁ
ŁŹčČ16ÖÖÇéżöĄŁ
ŒÇÖÁÉÙÓĐÒ»ÈËÄêÁäÔÚ[55,65Ł©ËêÎȘÊÂŒț![]() ŁŹÔò
ŁŹÔò![]()
ĄàÖÁÉÙÓĐÒ»ÈËÄêÁäÔÚ[55,65Ł©ËêÖźŒä”ÄžĆÂÊÎȘ![]() .
.

 ĂûÌâœđŸíÏ”ÁĐŽđ°ž
ĂûÌâœđŸíÏ”ÁЎ𰞥ŸÌâÄżĄżÄłżÆŒŒĐËÈ€ĐĄŚé¶ÔÖçÒčÎÂČî”ÄŽóĐĄÓëĐĄÂóĐÂÆ·ÖÖ·ąŃż¶àÉÙÖźŒä”ÄčŰÏ”œűĐĐÁËŃĐŸżŁŹŒÇÂŒÁË2016Äê12ÔÂ1ÈŐÖÁ12ÔÂ5ÈŐÎćÌì”ÄÖçÒčÎÂČîÓëÏàÓŠĂżÌì100żĆÖ֌ӔķąŃż”Ă”œÁËÈçÏÂÊęŸĘŁș
ÈŐÆÚ | 12ÔÂ1ÈŐ | 12ÔÂ2ÈŐ | 12ÔÂ3ÈŐ | 12ÔÂ4ÈŐ | 12ÔÂ5ÈŐ |
ÎÂČî | 9 | 11 | 10 | 12 | 13 |
·ąŃżÊę | 21 | 34 | 26 | 36 | 40 |
ÏÖŽÓŐâ5ŚéÊęŸĘÖĐÈÎŃĄÁœŚéŁŹÓĂÓàÏ”ÄÈęŚéÊęŸĘÇó»ŰčéÖ±Ïß·œłÌŁŹÔÙ¶Ô±»ŃĄÈĄ”ÄÁœŚéÊęŸĘœűĐĐŒìŃé.
ŁšąńŁ©ÇóŃĄÈĄ”ÄÁœŚéÊęŸĘÇĄșĂÊÇČ»ÏàÁÚ”ÄÁœÌì”ÄžĆÂÊŁ»
ŁšąòŁ©ÈôŃĄÈĄ”ÄÊÇ12ÔÂ1ÈŐșÍ12ÔÂ5ÈŐ”ÄÁœŚéÊęŸĘŁŹÇëžùŸĘÓàÏ”ÄÈęŚéÊęŸĘŁŹÇółö![]() Óë
Óë![]() ”ÄÏßĐÔ»ŰčéÖ±Ïß·œłÌ
”ÄÏßĐÔ»ŰčéÖ±Ïß·œłÌ![]() Ł»
Ł»
ŁšąóŁ©ÈôÓÉÏßĐÔ»ŰčéÖ±Ïß·œłÌ”Ă”œ”ÄčÀŒÆÖ”ÓëËùŃĄłö”ÄÁœŚéÊ”ŒÊÊęŸĘ”ÄÎóČîŸùČ»łŹčęÁœżĆŁŹÔòÈÏÎȘ”Ă”œ”Ä»ŰčéÖ±Ïß·œłÌÊǿɿż”ÄŁŹÊÔĆĐ¶ÏŁšąòŁ©ÖДÔœ”ÄÏßĐÔ»ŰčéÖ±Ïß·œłÌÊÇ·ńżÉżż.
žœŁșÔÚÏßĐÔ»Űčé·œłÌ![]() ÖĐŁŹ
ÖĐŁŹ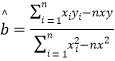 .
.