题目内容
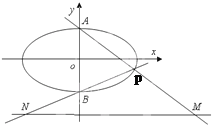
【题目】如图,已知椭圆![]() 的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线
的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线![]() 分别交于点M,N,
分别交于点M,N,
(1)设直线AP,BP的斜率分别为![]() ,求证:
,求证: ![]() 为定值;
为定值;
(2)求线段MN的长的最小值;
(3)当点P运动时,以MN为直径的圆是否经过某定点?请证明你的结论.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ) ![]() 随点
随点![]() 运动而变化,故设点
运动而变化,故设点![]() 表示
表示![]() ,进而化简整体消去变量;(Ⅱ)点
,进而化简整体消去变量;(Ⅱ)点![]() 的位置由直线
的位置由直线![]() ,
, ![]() 生成,所以可用两直线方程解出交点坐标,求出
生成,所以可用两直线方程解出交点坐标,求出![]() ,它必是
,它必是![]() 的函数,利用基本不等式求出最小值; (Ⅲ)利用
的函数,利用基本不等式求出最小值; (Ⅲ)利用![]() 的坐标求出圆的方程,方程必含有参数
的坐标求出圆的方程,方程必含有参数![]() ,消去一个后,利用等式恒成立方法求出圆所过定点坐标.
,消去一个后,利用等式恒成立方法求出圆所过定点坐标.
试题解析:(Ⅰ) ![]() ,令
,令![]() ,则由题设可知
,则由题设可知![]() ,
,
∴直线![]() 的斜率
的斜率![]() ,
, ![]() 的斜率
的斜率![]() ,又点
,又点![]() 在椭圆上,
在椭圆上,
所以![]() ,(
,( ![]() ),从而有
),从而有![]() .
.
(Ⅱ)由题设可以得到直线![]() 的方程为
的方程为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
由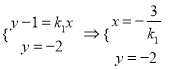 , 由
, 由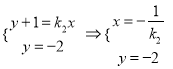 ,
,
![]() 直线
直线 ![]() 与直线
与直线![]() 的交点
的交点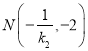 ,直线
,直线![]() 与直线
与直线![]() 的交点
的交点![]() .
.
又![]() ,
,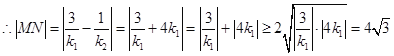
等号当且仅当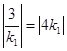 即
即![]() 时取到,故线段
时取到,故线段![]() 长的最小值是
长的最小值是![]() .
.
(Ⅲ)设点![]() 是以
是以![]() 为直径的圆上的任意一点,则
为直径的圆上的任意一点,则![]() ,故有
,故有
![]() ,又
,又![]() ,所以以
,所以以![]() 为直径的圆的方程为
为直径的圆的方程为
![]() ,令
,令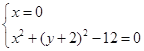 解得
解得 ,
,
以![]() 为直径的圆是否经过定点
为直径的圆是否经过定点![]() 和
和![]() .
.

练习册系列答案
相关题目
【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)若从这![]() 天中随机抽取两天,求至少有
天中随机抽取两天,求至少有![]() 天参加抽奖人数超过
天参加抽奖人数超过![]() 的概率;
的概率;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计若该活动持续
,并估计若该活动持续![]() 天,共有多少名顾客参加抽奖.
天,共有多少名顾客参加抽奖.
参考公式: 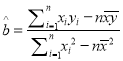 ,
, ![]() .
.