题目内容
10.直线l:x-2y+2=0过椭圆的上焦点F1和一个顶点B,该椭圆的离心率为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
分析 通过直线方程可得F1(0,1),B(-2,0),利用离心率计算公式计算即可.
解答 解:直线l:x-2y+2=0与坐标轴的交点为:(0,1),(-2,0),
由题可知:F1(0,1),B(-2,0),
∴c=1,b=2,
∴a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴e=$\frac{c}{a}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
故选:A.
点评 本题考查求椭圆的离心率,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
5.若多项式x2+x10=a0+a1(x+1)+…+a8(x+1)8+a9(x+1)9+a10(x+1)10,则a8=( )
| A. | 45 | B. | 9 | C. | -45 | D. | -9 |
19.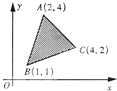 已知A(2,4),B(1,1),C(4,2).给出平面区域为三角形ABC的内部及其边界,若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a值等于( )
已知A(2,4),B(1,1),C(4,2).给出平面区域为三角形ABC的内部及其边界,若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a值等于( )
 已知A(2,4),B(1,1),C(4,2).给出平面区域为三角形ABC的内部及其边界,若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a值等于( )
已知A(2,4),B(1,1),C(4,2).给出平面区域为三角形ABC的内部及其边界,若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a值等于( )| A. | $\frac{1}{3}$ | B. | 6 | C. | 3 | D. | 1 |
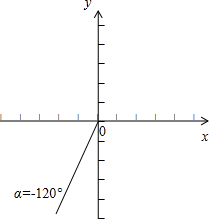 .
.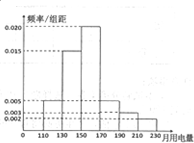 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.