题目内容
2.正三角形ABC的边长为4,将它沿高AD翻折,使得点B与点C的距离为2,此时四面体ABCD的外接球的表面积为$\frac{52π}{3}$.分析 三棱锥B-ACD的三条侧棱BD⊥AD、DC⊥DA,底面是正三角形,它的外接球就是它扩展为正三棱柱的外接球,求出正三棱柱的底面中心连线的中点到顶点的距离,就是球的半径,然后求球的表面积即可.
解答 解:根据题意可知三棱锥B-ACD的三条侧棱BD⊥AD、DC⊥DA,底面是正三角形,它的外接球就是它扩展为正三棱柱的外接球,求出正三棱柱的底面中心连线的中点到顶点的距离,就是球的半径,
正三棱柱ABC-A1B1C1的中,底面边长为1,棱柱的高为$2\sqrt{3}$,
由题意可得:三棱柱上下底面中点连线的中点,到三棱柱顶点的距离相等,说明中心就是外接球的球心,
∴正三棱柱ABC-A1B1C1的外接球的球心为O,外接球的半径为r,表面积为:4πr2.
球心到底面的距离为$\sqrt{3}$,
底面中心到底面三角形的顶点的距离为:$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$×2=$\frac{2\sqrt{3}}{3}$,
所以球的半径为r=$\sqrt{({\sqrt{3})}^{2}+(\frac{2\sqrt{3}}{3})^{2}}$=$\sqrt{\frac{13}{3}}$.
外接球的表面积为:4πr2=$\frac{52π}{3}$.
故答案为:$\frac{52π}{3}$.
点评 本题考查空间想象能力,计算能力;三棱柱上下底面中点连线的中点,到三棱柱顶点的距离相等,说明中心就是外接球的球心,是本题解题的关键,仔细观察和分析题意,是解好数学题目的前提.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.直线l:x-2y+2=0过椭圆的上焦点F1和一个顶点B,该椭圆的离心率为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
7. 某校高三年级100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100],这100名学生数学成绩在[70,100]分数段内的人数为( )
某校高三年级100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100],这100名学生数学成绩在[70,100]分数段内的人数为( )
 某校高三年级100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100],这100名学生数学成绩在[70,100]分数段内的人数为( )
某校高三年级100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100],这100名学生数学成绩在[70,100]分数段内的人数为( )| A. | 60 | B. | 55 | C. | 50 | D. | 45 |
14.下列各组中的两个函数是同一函数的是( )
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$和f(x)=x+1 | |
| B. | f(r)=πr2(r≥0)和g(x)=πx2(x≥0) | |
| C. | f(x)=logaax(a>0且a≠1)和g(x)=${a}^{lo{g}_{a}x}$(a>0且a≠1) | |
| D. | f(x)=x和g(t)和g(t)=$\sqrt{{t}^{2}}$ |
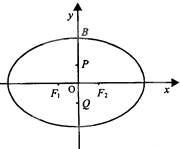 如图:设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左,右两个焦点分别为F1,F2,短轴的上端点为B,短轴上的两个三等分点为P,Q,且F1PF2Q为正方形,若过点B作此正方形的外接圆的切线在x轴上的一个截距为-$\frac{3\sqrt{2}}{4}$,则此椭圆方程的方程为$\frac{x^2}{10}+\frac{y^2}{9}=1$.
如图:设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左,右两个焦点分别为F1,F2,短轴的上端点为B,短轴上的两个三等分点为P,Q,且F1PF2Q为正方形,若过点B作此正方形的外接圆的切线在x轴上的一个截距为-$\frac{3\sqrt{2}}{4}$,则此椭圆方程的方程为$\frac{x^2}{10}+\frac{y^2}{9}=1$.