题目内容
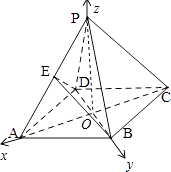
【题目】如图,正四棱锥P﹣ABCD中,底面ABCD的边长为4,PD=4,E为PA的中点, 
(1)求证:平面EBD⊥平面PAC;
(2)求直线BE与平面PBD所成角的正弦值.
【答案】
(1)证明:设AC,BD交点为O,连结PO.则O为正方形ABCD的中心,
∴PO⊥平面ABCD.∵BD平面ABCD,
∴PO⊥BD.
∵四边形ABCD是正方形,∴BD⊥AC.
又AC平面PAC,PO平面PAC,AC∩PO=O,
∴BD⊥平面PAC,又BD平面EBD,
∴平面EBD⊥平面PAC.
(2)解:以O为原点,以OA,OB,OP为坐标轴建立空间直角坐标系,
∵正四棱锥的棱长为4,∴OA=OB=OD=2 ![]() ,OP=
,OP= ![]() =2
=2 ![]() .
.
∴A(2 ![]() ,0,0),B(0,2
,0,0),B(0,2 ![]() ,0),P(0,0,2
,0),P(0,0,2 ![]() ),∴E(
),∴E( ![]() ,0,
,0, ![]() ).
).
∴ ![]() =(
=( ![]() ,﹣2
,﹣2 ![]() ,
, ![]() ).
).
显然x轴⊥平面PBD.∴ ![]() =(1,0,0)是平面PBD的一个法向量,
=(1,0,0)是平面PBD的一个法向量,
∴ ![]() =
= ![]() ,|
,| ![]() |=1,|
|=1,| ![]() |=2
|=2 ![]() .
.
∴cos< ![]() >=
>= 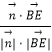 =
= ![]() .
.
∴直线BE与平面PBD所成角的正弦值为 ![]() .
.
【解析】(1)设AC,BD交点为O,连结PO,则PO⊥平面ABCD,于是PO⊥BD,又BD⊥AC,故而BD⊥平面PAC,于是平面EBD⊥平面PAC;(2)以O为原点,以OA,OB,OP为坐标轴建立空间直角坐标系,则 ![]() =(1,0,0)为平面PBD的一个法向量,求出cos<
=(1,0,0)为平面PBD的一个法向量,求出cos< ![]() ,
, ![]() >,则|cos<
>,则|cos< ![]() ,
, ![]() >|即为所求.
>|即为所求.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则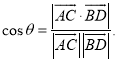 .
.

练习册系列答案
相关题目



