题目内容
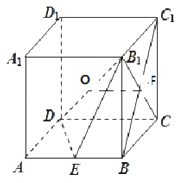
【题目】如图，在正方体ABCD﹣A1B1C1D1的棱长为a，若E为棱AB的中点，
①求四棱锥B1﹣BCDE的体积
②求证：面B1DC⊥面B1DE．
【答案】①
；②见解析.
【解析】试题分析：
①由正方体的性质可得B1B⊥平面BEDC，结合棱锥的体积公式计算可得四棱锥B1﹣BCDE的体积V=
；
②取B1D的中点O，设BC1∩B1C=F，连接OF，由题意可得四边形OEBF是平行四边形，结合正方体的性质可得OE⊥DC，OE⊥B1C，故OE⊥平面B1DC，结合面面垂直的判断定理可得平面B1DC⊥面B1DE．
试题解析：
①由正方体的性质可得B1B⊥平面BEDC，
∴四棱锥B1﹣BCDE的体积V=
S梯形BCDEB1B=
（a+a）aa=
；
②取B1D的中点O，设BC1∩B1C=F，连接OF，
∵O，F分别是B1D与B1C的中点，∴OF∥DC，且OF=DC，
又∵E为AB中点，∴EB∥DC，且EB=DC，
∴OF∥EB，OF=EB，即四边形OEBF是平行四边形，∴OE∥BF，
∵DC⊥平面BCC1B1 ， BC1平面BCC1B1 ， ∴BC1⊥DC，∴OE⊥DC．
又BC1⊥B1C，∴OE⊥B1C，又∵DC平面B1DC，B1C平面B1DC，DC∩B1C=C，
∴OE⊥平面B1DC，又∵OE平面B1DE，∴平面B1DC⊥面B1DE．
练习册系列答案
相关题目
