题目内容
15.数列{an}的前n项和记为 Sn,a1=2,an+1=Sn+n,等差数列{bn}的各项为正,其前n项和为Tn,且 T3=9,又 a1+b1,a2+b2,a3+b3成等比数列.(Ⅰ)求{an},{bn}的通项公式;
(Ⅱ)求证:当n≥2时,$\frac{1}{{{b}_{1}}^{2}}$+$\frac{1}{{{b}_{2}}^{2}}$+…+$\frac{1}{{{b}_{n}}^{2}}$<$\frac{5}{4}$.
分析 (Ⅰ)由an+1=Sn+n,得an=Sn-1+(n-1)(n≥2),两式相减,结合等比数列的定义和通项,即可得到{an}的通项;再由等比数列的性质,求得等差数列{bn}的首项和公差,即可得到所求通项;
(Ⅱ)$\frac{1}{{{b}_{k}}^{2}}$=$\frac{1}{(2k-1)^{2}}$<$\frac{1}{(2k-1)^{2}-1}$=$\frac{1}{4k(k-1)}$=$\frac{1}{4}$($\frac{1}{k-1}$-$\frac{1}{k}$),再由裂项相消求和,结合不等式的性质,即可得证.
解答 解:(Ⅰ)由an+1=Sn+n,得
an=Sn-1+(n-1)(n≥2),两式相减得
an+1-an=Sn-Sn-1+1=an+1,所以an+1=2an+1,
所以an+1+1=2(an+1)(n≥2),
又a2=3所以an+1=2n-2(a2+1),从而an=2n-1(n≥2),
而a1=2,不符合上式,所以an=$\left\{\begin{array}{l}{2,n=1}\\{{2}^{n}-1,n≥2}\end{array}\right.$;
因为{bn}为等差数列,且前三项的和T3=9,所以b2=3,
可设b1=3-d,b3=3+d,由于a1=2,a2=3,a3=7,
于是a1+b1=5-d,a2+b2=6,a3+b3=10+d,
因为a1+b1,a2+b2,a3+b3成等比数列.
所以(5-d)(10+d)=36,d=2或d=-7(舍),
所以bn=b1+(n-1)d=1+2(n-1)=2n-1;
(Ⅱ)证明:因为$\frac{1}{{{b}_{k}}^{2}}$=$\frac{1}{(2k-1)^{2}}$<$\frac{1}{(2k-1)^{2}-1}$=$\frac{1}{4k(k-1)}$=$\frac{1}{4}$($\frac{1}{k-1}$-$\frac{1}{k}$)
所以,当n≥2时,$\frac{1}{{{b}_{1}}^{2}}$+$\frac{1}{{{b}_{2}}^{2}}$+…+$\frac{1}{{{b}_{n}}^{2}}$=$\frac{1}{{1}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{(2k-1)^{2}}$
<1+$\frac{1}{4}$[(1-$\frac{1}{2}$)+($\frac{1}{2}-\frac{1}{3}$)+…+($\frac{1}{n-1}$-$\frac{1}{n}$)]
=1+$\frac{1}{4}$(1-$\frac{1}{n}$)<1+$\frac{1}{4}$=$\frac{5}{4}$.
则有当n≥2时,$\frac{1}{{{b}_{1}}^{2}}$+$\frac{1}{{{b}_{2}}^{2}}$+…+$\frac{1}{{{b}_{n}}^{2}}$<$\frac{5}{4}$.
点评 本题考查等差数列和等比数列的通项和求和公式的运用,同时考查不等式的放缩法和裂项相消求和的运用,考查运算能力,属于中档题.

| A. | 直线y=0对称 | B. | 直线x=0对称 | C. | 直线y=1对称 | D. | 直线x=1对称 |
| A. | (0,1) | B. | (1,2) | C. | (2,e) | D. | (3,4) |
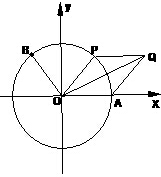 如图,点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$).
如图,点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$).