题目内容
19.将9个相同的小球放入3个不同的盒子,要求每个盒子中至少有一个小球,且每个盒子里的小球个数都不相同,则不同的放法种数为( )| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
分析 根据题意,先用挡板法分析每个盒子中至少有1个小球的情况数目,再分类讨论有盒子中的小球个数相同的放法,利用间接法可得结论
解答 解:先考虑每个盒子中至少有1个小球,
用挡板法,9个球中间8个空,插入两个板,共有C82=28种,
其中每个盒子中的小球个数都相同时,有1种放法;
两个盒子中的小球个数都相同时,包括:1、1、7;2、2、5;4、4、1,三种情况,每种情况各有3种放法,共9种放法;
所以不同的放法共有28-1-9=18种放法;
故选:C.
点评 本题考查排列、组合的应用,利用间接法分析可以避免大量的分类讨论与复杂的计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若向量$\overrightarrow a,\vec b$满足$|{\vec a}|=1,|{\vec b}|=2$且$|{2\vec a+\vec b}|=2\sqrt{3}$,则向量$\overrightarrow a,\vec b$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
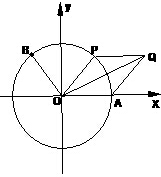 如图,点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$).
如图,点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$). 甲、乙两人在9天每天加工零件的个数用茎叶图表示如图,则这9天甲、乙加工零件个数的中位数之和为91.(考点:茎叶图与中位数综合)
甲、乙两人在9天每天加工零件的个数用茎叶图表示如图,则这9天甲、乙加工零件个数的中位数之和为91.(考点:茎叶图与中位数综合)