题目内容
20．教室内有一把直尺，无论这把直尺怎样放置，在教室的地面上总能画出一条直线，使这条直线与直尺（ ）| A． | 平行 | B． | 垂直 | C． | 异面 | D． | 相交 |
分析 由题设条件可知，可以借助投影的概念对及三垂线定理选出正确选项．
解答 解：由题意，直尺所在直线若与地面垂直，则在地面总有这样的直线，使得它与直尺所在直线垂直
若直尺所在直线若与地面不垂直，则其必在地面上有一条投影线，在平面中一定存在与此投影线垂直的直线，由三垂线定理知，与投影垂直的直线一定与此斜线垂直
综上，教室内有一直尺，无论怎样放置，在地面总有这样的直线，使得它与直尺所在直线垂直
故选：B．
点评 本题考查空间中直线与平面之间的位置关系，解题的关键是熟练掌握线面垂直与三垂线定理，再结合直线与地面位置关系的判断得出答案．
练习册系列答案
相关题目
11．若向量$\overrightarrow a，\vec b$满足$|{\vec a}|=1，|{\vec b}|=2$且$|{2\vec a+\vec b}|=2\sqrt{3}$，则向量$\overrightarrow a，\vec b$的夹角为（ ）
| A． | $\frac{2π}{3}$ | B． | $\frac{π}{2}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{6}$ |
甲、乙两人在9天每天加工零件的个数用茎叶图表示如图，则这9天甲、乙加工零件个数的中位数之和为91．（考点：茎叶图与中位数综合）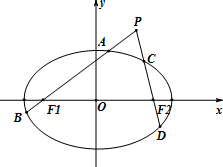
如图，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点分别为F1，F2，离心率为$\frac{{\sqrt{2}}}{2}$，它的四个顶点连成的菱形的面积为8$\sqrt{2}$．过动点P（不在x轴上）的直线PF1，PF2与椭圆的交点分别为A，B和C，D．