题目内容
已知函数 ,若
,若 在
在 上的最小值记为
上的最小值记为 .
.
(1)求 ;
;
(2)证明:当 时,恒有
时,恒有 .
.
 ,若
,若 在
在 上的最小值记为
上的最小值记为 .
.(1)求
 ;
;(2)证明:当
 时,恒有
时,恒有 .
.(1)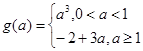 ;(2)详见解析.
;(2)详见解析.
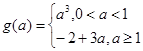 ;(2)详见解析.
;(2)详见解析.试题分析:(1)因为
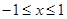 ,对实数
,对实数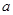 分类讨论,①
分类讨论,①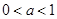 ,②
,②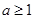 ,分别用导数法求函数
,分别用导数法求函数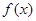 单调区间,从而确定
单调区间,从而确定 的值,再用分段函数表示
的值,再用分段函数表示 ;(2)构造函数
;(2)构造函数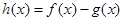 ,对实数
,对实数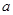 分类讨论,①
分类讨论,①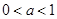 ,②
,②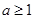 ,分别用导数法求函数
,分别用导数法求函数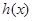 单调区间,从而确定
单调区间,从而确定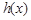 的最大值,即可证明当
的最大值,即可证明当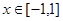 时恒有
时恒有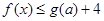 成立.
成立.(1)因为
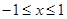 ,
,①当
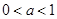 时,
时,若
 ,则
,则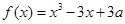 ,
,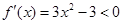 ,故
,故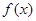 在
在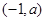 上是减函数;
上是减函数;若
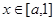 ,则
,则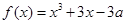 ,
,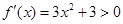 ,故
,故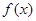 在
在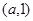 上是增函数;
上是增函数;所以,
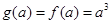 .
.②当
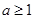 ,则
,则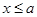 ,
,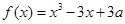 ,
,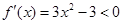 ,故
,故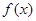 在
在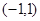 上是减函数,
上是减函数,所以
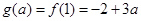 ,
,综上所述,
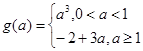 .
.(2)令
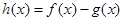 ,
,①当
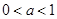 时,
时,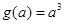 ,
,若
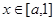 ,
,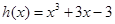 得
得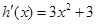 ,所以
,所以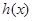 在
在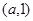 上是增函数,所以
上是增函数,所以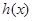 在
在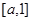 上的最大值是
上的最大值是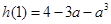 ,且
,且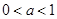 ,所以
,所以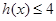 ,
,故
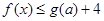 .
.若
 ,
,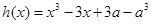 ,则
,则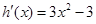 ,所以
,所以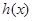 在
在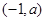 上是减函数,
上是减函数,所以
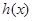 在
在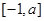 上的最大值是
上的最大值是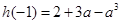 ,
,令
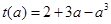 ,则
,则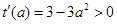 ,
,所以
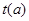 在
在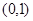 上是增函数,所以
上是增函数,所以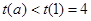 即
即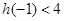 ,
,故
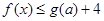 ,
,②当
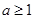 时,
时,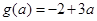 ,所以
,所以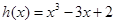 ,得
,得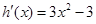 ,
,此时
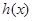 在
在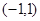 上是减函数,因此
上是减函数,因此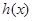 在
在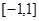 上的最大值是
上的最大值是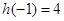 ,
,故
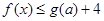 ,
,综上所述,当
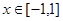 时恒有
时恒有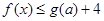 .
.
练习册系列答案
相关题目
 x2+4x-3ln x在[t,t+1]上不单调,则t的取值范围是________.
x2+4x-3ln x在[t,t+1]上不单调,则t的取值范围是________. 平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为
平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为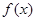 元.
元.
 在
在 上的最大值和最小值分别记为
上的最大值和最小值分别记为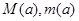 ,求
,求 ;
; 若
若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.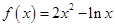 的递增区间是( )
的递增区间是( )



 x3+
x3+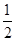 x2+2ax,若f(x)在(
x2+2ax,若f(x)在(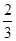 ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )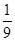
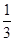 x3-x2-3x+
x3-x2-3x+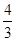 ,直线l:9x+2y+c=0,若当x∈[-2,2]时,函数y=f(x)的图象恒在直线l下方,则c的取值范围是________.
,直线l:9x+2y+c=0,若当x∈[-2,2]时,函数y=f(x)的图象恒在直线l下方,则c的取值范围是________.