题目内容
已知函数f（x）=lnx+tanα（α∈（0，
））的导函数为f′（x），若使得f′（x0）=f（x0）立的x0＜1，则实数α的取值范围为（ ）
| π |
| 2 |
A．（
| B．（0，
| C．（
| D．（0，
|
∵f′（x）=
，f′（x0）=
，f′（x0）=f（x0），
∴
=lnx0+tanα，
∴tanα=
-lnx0，
又∵0＜x0＜1，
∴可得
-lnx0＞1，即tanα＞1，
∴α∈（
，
）．
故选：A．
| 1 |
| x |
| 1 |
| x0 |
∴
| 1 |
| x0 |
∴tanα=
| 1 |
| x0 |
又∵0＜x0＜1，
∴可得
| 1 |
| x0 |
∴α∈（
| π |
| 4 |
| π |
| 2 |
故选：A．
练习册系列答案
学业测评一课一测系列答案
相关题目
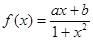是定义在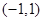
上的奇函数，且
.
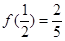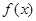的解析式；
.
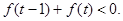，函数
.
时，函数
的图象与函数
的图象有公共点，求实数
的最大值；
时，试判断函数
的上方？若能，求出
的取值范围；若不能，请说明理由．
.
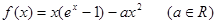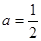时,求函数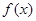
的单调区间;
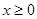时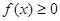
,求a的取值范围.
，若
在
上的最小值记为
.
时，恒有
.