题目内容
11．二面角α-l-β的半平面α内有一条直线a与棱l成45°角，若二面角的大小也为45°，则直线a与平面β所成角的大小为30°．分析 先根据题意画出相应的图形，然后找出AB与面β的所成角，在直角三角形ABD中进行求解即可．
解答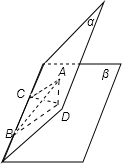 
解：根据题意先画出图形作AD⊥β交面β于D
由题意可知∠ABC=45°，∠ACD=45°
设AD=1，则CD=1，AC=$\sqrt{2}$，BC=$\sqrt{2}$，AB=2
而AD=1，三角形ABD为直角三角形
∴∠ABD=30°
故答案为：30°．
点评 本题主要考查了直线与平面所成角的度量，解题的关键是通过题意画出相应的图象，属于中档题．
练习册系列答案
相关题目
19．设F1、F2是双曲线$\frac{{x}^{2}}{4a}$-$\frac{{y}^{2}}{a}$=1（a＞0）的两个焦点，点P在双曲线上，且$\overrightarrow{PF1}$•$\overrightarrow{PF2}$=0，|$\overrightarrow{PF1}$|•|$\overrightarrow{PF2}$|=2，则a的值等于（ ）
| A． | 2 | B． | 1 | C． | $\frac{\sqrt{5}}{2}$ | D． | $\sqrt{5}$ |
6．若a＞b＞0，则下列不等式成立的是（ ）
| A． | a＞b＞$\frac{a+b}{2}$＞$\sqrt{ab}$ | B． | a＞$\frac{a+b}{2}$＞$\sqrt{ab}$＞b | C． | a＞$\frac{a+b}{2}$＞b＞$\sqrt{ab}$ | D． | a＞$\frac{a+b}{2}$≥$\sqrt{ab}$＞b |
16．直线x+2y+1=0被圆（x-2）2+（y-1）2=25所截得的弦长为（ ）
| A． | 5$\sqrt{5}$ | B． | 4$\sqrt{5}$ | C． | 3$\sqrt{5}$ | D． | $2\sqrt{5}$ |
20．
如图所示，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=30°以及∠MAC=105°；从C点测得∠MCA=45°．已知山高BC=150米，则所求山高MN为（ ）米．
如图所示，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=30°以及∠MAC=105°；从C点测得∠MCA=45°．已知山高BC=150米，则所求山高MN为（ ）米．| A． | 300$\sqrt{3}$ | B． | 150$\sqrt{6}$ | C． | 150$\sqrt{3}$ | D． | 300$\sqrt{6}$ |
如图，△ABC为直角三角形，∠ABC=90°，以AB为直径的圆交AC与点E，点D是BC边的中点，连接OD交圆于点M，求证：