题目内容
20.若点(p,q),在|p|≤3,|q|≤3中按均匀分布出现,则方程x2+2px-q2+1=0有两个实数根的概率$\frac{36-π}{36}$.分析 由题意,本题符合几何概型,只要求出点(p,q)对应区域的面积,利用公式解答.
解答  解:点(p,q),在|p|≤3,|q|≤3中按均匀分布出现,对应区域的面积为6×6=36,
解:点(p,q),在|p|≤3,|q|≤3中按均匀分布出现,对应区域的面积为6×6=36,
由方程x2+2px-q2+1=0有两个实数根得到4p2+4q2-4≥0,即p2+q2≥1,对应区域面积为π,如图
根据几何概型的概率公式得到方程x2+2px-q2+1=0有两个实数根的概率:$\frac{36-π}{36}$;
故答案为:$\frac{36-π}{36}$.
点评 本题考查了几何概型概率的求法;关键是明确点(p,q)对应的区域面积.

练习册系列答案
相关题目
11.函数f(x)=3x3-9x2+5在区间[-2,2]上的最大值是( )
| A. | 5 | B. | 2 | C. | -7 | D. | 14 |
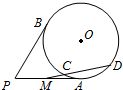 如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=8,MC=2,则CD=6.
如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=8,MC=2,则CD=6.