题目内容

【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员名,其中种子选手名;乙协会的运动员名,其中种子选手名.从这名运动员中随机选择人参加比赛.

(1)设为事件“选出的人中恰有名种子选手,且这名种子选手来自同一个协会”求事件发生的概率;

(2)设为选出的人中种子选手的人数,求随机变量的分布列和数学期望.

【答案】（1）（2）分布列见解析，

【解析】试题分析：（1）从这名运动员中随机选择人参加比赛有种方法，而事件A包含种方法，最后根据古典概型概率求法得概率（2）先确定随机变量取法为，再利用组合求出对应概率。列表可得分布列，最后根据数学期望公式求期望

试题解析：解：（I）由已知，有，

所以事件发生的概率为

（II）随机变量的所有可能取值为

.

所以，随机变量的分布列为

x

1

2

3

4

P

随机变量的数学期望

练习册系列答案
相关题目

【题目】(1)向量a＝(x,1)，b＝(1，y)，c＝(2，－4)，且a⊥c，b∥c，求|a＋b|和a＋b与c的夹角；

(2)设O为△ABC的外心，已知AB＝3，AC＝4，非零实数x，y满足＝x＋y，且x＋2y＝1，求cos ∠BAC的值．

【题目】已知函数f(x)＝ax3－bx2＋(2－b)x＋1在x＝x1处取得极大值，在x＝x2处取得极小值，且0＜x1＜1＜x2＜2.

(1)证明：a＞0；

(2)若z＝a＋2b，求z的取值范围.

【题目】某商品的进价为每件元，售价为每件元，每个月可卖出件；如果每件商品在该售价的基础上每上涨元，则每个月少卖件（每件售价不能高于元）.设每件商品的售价上涨元（为正整数），每个月的销售利润为元.

（1）求与的函数的函数关系式并直接写出自变量的取值范围；

（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

【题目】2017年1月1日，作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间，为了活跃气氛，主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查，统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况，具体数据如图表：

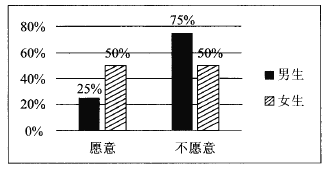
（1）根据条件完成下列列联表，并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关？

愿意

不愿意

总计

男生

女生

总计

（2）现用分层抽样的方法从愿意接受挑战的市民中选取7名挑战者，再从中抽取2人参加挑战，求抽取的2人中至少有一名男生的概率.

参考数据及公式：

0.1

0.05

0.025

0.01

2.706

3.841

5.024

6.635

.

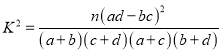【题目】已知函数f(x)＝5x＋x－2，g(x)＝log5x＋x－2的零点分别为x1，x2，则x1＋x2的值为________．

【题目】网络购物已经成为一种时尚，电商们为了提升知名度，加大了在媒体上的广告投入．经统计，近五年某电商在媒体上的广告投入费用x（亿元）与当年度该电商的销售收入y（亿元）的数据如下表：）：

年份

2012年

2013年

2014

2015

2016

广告投入x

0.8

0.9

1

1.1

1.2

销售收入y

16

23

25

26

30

（1）求y关于x的回归方程； （2）2017年度该电商准备投入广告费1.5亿元，

利用（1）中的回归方程，预测该电商2017年的销售收入．

附：回归直线的斜率和截距的最小二乘估计公式分别为：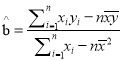

，选用数据： ，

【题目】过点作抛物线的两条切线, 切点分别为, .

（1） 证明: 为定值;

（2） 记△的外接圆的圆心为点, 点是抛物线的焦点, 对任意实数, 试判断以为直径的圆是否恒过点? 并说明理由.

【题目】已知f(x)＝2sin(x－)－，现将f(x)的图象向左平移个单位长度，再向上平移个单位长度，得到函数g(x)的图象．

(1)求f()＋g()的值；

(2)若a，b，c分别是△ABC三个内角A，B，C的对边，a＋c＝4，且当x＝B时，g(x)取得最大值，求b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网